Эллипс

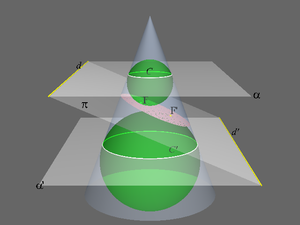
Не следует путать с Эллипсис.

Эллипс, его фокусы и главные оси

Эллипс как коническое сечение, его фокусы и директрисы, получаемые геометрически с помощью шаров Данделена.

Э́ллипс (др.-греч. ἔλλειψις — опущение, недостаток, в смысле недостатка эксцентриситета до 1) — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек $F_1$ и $F_2$ (называемых фокусами) постоянна и больше расстояния между фокусами, то есть

$|F_1M|+|F_2M|=2a,$ причем $|F_1F_2|<2a.$

Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой.

Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.

Связанные определения

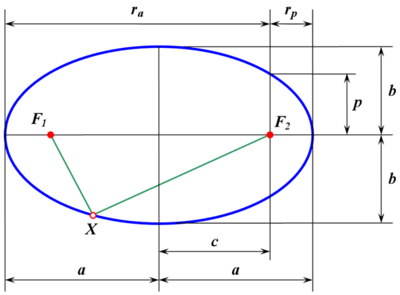
• Проходящий через фокусы эллипса отрезок AB, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
• Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
• Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
• Точка пересечения большой и малой осей эллипса называется его центром.
• Расстояния $r_1$ и $r_2$ от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
• Расстояние $c=\frac{|F_1 F_2|}{2}$ называется фокальным расстоянием.
• Величина $e = \frac{c}{a} = \sqrt{1 - \frac{b^2}{a^2}}$ называется эксцентриситетом.
• Диаметром эллипса называют произвольную хорду, проходящую через его центр. Сопряжёнными диаметрами эллипса называют пару его диаметров, обладающих следующим свойством: середины хорд, параллельных первому диаметру, лежат на втором диаметре. В этом случае и середины хорд, параллельных второму диаметру, лежат на первом диаметре.
• Радиус эллипса в данной точке (расстояние от его центра до данной точки) вычисляется по формуле $r=\frac{ab}{\sqrt{b^2 \cos^2\varphi + a^2 \sin^2\varphi}} = \frac{b}{\sqrt{1 - e^2 \cos^2\varphi}}$, где $\varphi$ — угол между радиус-вектором данной точки и осью абсцисс.
• Фокальным параметром $p=\frac{b^2}{a}$ называется половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса.
• Отношение длин малой и большой полуосей называется коэффициентом сжатия эллипса или эллиптичностью: $k = \frac{b}{a}.$ Величина, равная $(1-k) = \frac{a-b}{a},$ называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент сжатия и эксцентриситет эллипса связаны соотношением $~k^2=1-e^2.$
• Для каждого из фокусов существует прямая, называемая директрисой, такая, что отношение расстояния от произвольной точки эллипса до его фокуса к расстоянию от этой точки до данной прямой равно эксцентриситету эллипса. Весь эллипс лежит по ту же сторону от такой прямой, что и фокус. Уравнения директрис эллипса в каноническом виде записываются как $x = \pm\frac{p}{e\left(1+e\right)}$ для фокусов $\left(\mp\frac{p}{1+e},\,0\right)$ соответственно. Расстояние между фокусом и директрисой равно $\frac{p}{e}.$

Свойства

• Оптические
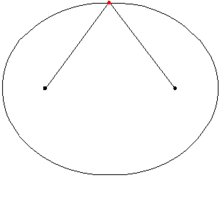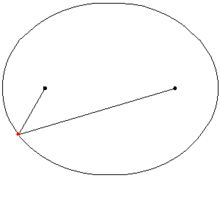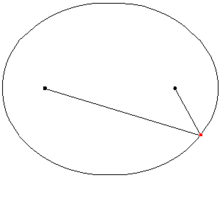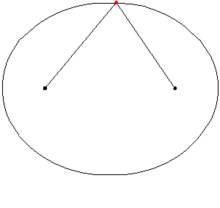
  • Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.
  • Свет от источника, находящегося вне любого фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.
• Если $F_1$ и $F_2$ — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой $(F_1X)$ равен углу между этой касательной и прямой $(F_2X)$.
• Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
• Эволютой эллипса является астроида.
• Точки пересечения эллипса с осями являются его вершинами.
• Эксцентриситет эллипса равен отношению $e = \frac{c}{a} = \sqrt{1 - \frac{b^2}{a^2}}\;\;\;(0 \leqslant e < 1).$ Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
• Эллипс также можно описать как
  • фигуру, которую можно получить из окружности, применяя аффинное преобразование
  • ортогональную проекцию окружности на плоскость.
  • Пересечение плоскости и кругового цилиндра

Соотношения между элементами эллипса

Части эллипса (описание см. в разделе "Связанные определения")

• $~\boldsymbol a$ — большая полуось;
• $~\boldsymbol b$ — малая полуось;
• $~\boldsymbol c$ — фокальный радиус (полурасстояние между фокусами);
• $~\boldsymbol p$ — фокальный параметр;
• $~\boldsymbol r_p$ — перифокусное расстояние (минимальное расстояние от фокуса до точки на эллипсе);
• $~\boldsymbol r_a$ — апофокусное расстояние (максимальное расстояние от фокуса до точки на эллипсе);

$~a^2 = b^2 + c^2$

$e = \frac{c}{a} = \sqrt{1 - \frac{b^2}{a^2}}\;\;\;(0 \leqslant e < 1).$.

$~p = \frac{b^2}{a}$

	$~\boldsymbol a$	$~\boldsymbol b$	$~\boldsymbol c$	$~\boldsymbol p$	$~\boldsymbol {r_p}$	$~\boldsymbol {r_a}$
$~\boldsymbol a$ – большая полуось	$~\boldsymbol a$	$~a = \frac{b}{\sqrt{1-e^2}}$	$~a = \frac{c}{e}$	$~a = \frac{p}{1-e^2}$	$~a = \frac{r_p}{1-e}$	$~a = \frac{r_a}{1+e}$
$~\boldsymbol b$ – малая полуось	$~b = a \sqrt{1-e^2}$	$~\boldsymbol b$	$~b = \frac{c~\sqrt{1-e^2}}{e}$	$~b = \frac{p}{\sqrt{1-e^2}}$	$~b = r_p\sqrt{\frac{1+e}{1-e}}$	$~b = r_a\sqrt{\frac{1-e}{1+e}}$
$~\boldsymbol c$ – фокальное расстояние	$~c = ae$	$~c = \frac{be}{\sqrt{1-e^2}}$	$~\boldsymbol c$	$~c = \frac{pe}{1-e^2}$	$~c = \frac{r_pe}{1-e}$	$~c = \frac{r_ae}{1+e}$
$~\boldsymbol p$ – фокальный параметр	$~p = a(1-e^2)$	$~p = b~\sqrt{1-e^2}$	$~p = c~\frac{1-e^2}{e}$	$~\boldsymbol p$	$~p = r_p (1+e)$	$~p = r_a (1-e)$
$~\boldsymbol r_p$ – перифокусное расстояние	$~r_p = a(1-e)$	$~r_p = b~\sqrt{\frac{1-e}{1+e}}$	$~r_p = c~\frac{1-e}{e}$	$~r_p = \frac{p}{1+e}$	$~\boldsymbol r_p$	$~r_p = r_a\frac{1-e}{1+e}$
$~\boldsymbol r_a$ – апофокусное расстояние	$~r_a = a(1+e)$	$~ r_a = b~\sqrt{\frac{1+e}{1-e}}$	$~ r_a = c~\frac{1+e}{e}$	$~ r_a = \frac{p}{1-e}$	$~ r_a = r_p~\frac{1+e}{1-e}$	$~\boldsymbol r_a$

Координатное представление

Эллипс как кривая второго порядка

Эллипс является центральной невырожденной кривой второго порядка и удовлетворяет общему уравнению вида

$~a_{11}x^2 + a_{22}y^2+2a_{12}xy+2a_{13}x+2a_{23}y+a_{33}=0,$

при инвариантах $D > 0\,$ и $\Delta I < 0,\,$ где:

$\Delta=\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{12} & a_{22} & a_{23} \\ a_{13} & a_{23} & a_{33} \end{vmatrix},$

$D=\begin{vmatrix} a_{11} & a_{12} \\ a_{12} & a_{22}\end{vmatrix}=a_{11}a_{22} - a_{12}^2,$

$I=tr\begin{pmatrix} a_{11} & a_{12} \\ a_{12} & a_{22}\end{pmatrix}=a_{11}+a_{22}.$

Соотношения между инвариантами кривой второго порядка и полуосями эллипса:

$\Delta = -\frac{1}{a^2}\frac{1}{b^2},\,$

$D = \frac{1}{a^2}\frac{1}{b^2},\,$

$I = \frac{1}{a^2}+\frac{1}{b^2}.\,$

Каноническое уравнение

Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):

$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1.$

Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат.

Соотношения  

Для определённости положим, что $0 < b \leqslant a.$ В этом случае величины $a$ и $b$ — соответственно, большая и малая полуоси эллипса.

Зная полуоси эллипса можно вычислить его фокальное расстояние и эксцентриситет:

$\left|F_1F_2\right|=2\sqrt{a^2-b^2},\;\;\;e=\frac{\sqrt{a^2-b^2}}{a}< 1.$

Координаты фокусов эллипса:

$\left(ae,\,0\right),\;\;\;\left(-ae,\,0\right).$

Эллипс имеет две директрисы, уравнения которых можно записать как

$x=\frac{a}{e},\;\;\;x=-\frac{a}{e}.$

Фокальный параметр (т.е. половина длины хорды, проходящей через фокус и перпендикулярной оси эллипса) равен

$p=\frac{b^2}{a}.$

Фокальные радиусы, т. е. расстояния от фокусов до произвольной точки кривой $\left(x,\,y\right):$

$r_1 = a + ex,\;\;\;r_2 = a - ex.$

Уравнение диаметра, сопряжённого хордам с угловым коэффициентом $k:$:

$y=-\frac{b^2}{a^2k}x.$

Уравнение касательной к эллипсу в точке $(x_0,y_0)$ имеет вид $:$

$\frac{xx_0}{a^2} + \frac{yy_0}{b^2} =1.$

Условие касания прямой $y=mx+k$ и эллипса $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ записывается в виде соотношения $:$ $k^2=m^2a^2 + b^2$

Уравнение касательных, проходящих через точку $\left(x_1, y_1\right):$

$\frac{y-y_1}{x-x_1}=\frac{-x_1y_1 \pm \sqrt{b^2x_1^2 + a^2y_1^2 - a^2b^2}}{a^2 - x_1^2}$

Уравнение касательных, имеющих данный угловой коэффициент $k:$:

$y=kx \pm \sqrt{k^2a^2 + b^2}.$

Уравнение нормали в точке $\left(x_1, y_1\right):$

$\frac{y-y_1}{x-x_1}=\frac{a^2y_1}{b^2x_1}.$

Уравнения в параметрической форме

Геометрическая иллюстрация параметризации эллипса (анимация).

Каноническое уравнение эллипса может быть параметризовано:

$\begin{cases} x = a\,\cos t \\ y = b\,\sin t \end{cases}\;\;\; 0 \leqslant t \leqslant 2\pi,$

где $t\,$ — параметр уравнения.

В случае окружности параметр $t\,$ является углом между радиус-вектором данной точки и положительным направлением оси абсцисс.

В полярных координатах

Если принять фокус эллипса за полюс, а большую ось — за полярную ось, то его уравнение в полярных координатах $\left(\rho, \varphi\right)$ будет иметь вид

$\rho = \frac{p}{1 \pm e \cos \varphi},$

где e — эксцентриситет, а p — фокальный параметр. При положительном знаке перед e второй фокус эллипса будет находиться в точке $\left(0, 2c\right),$ а при отрицательном — в точке $\left(\pi, 2c\right),$ где фокальное расстояние $c = \frac{pe}{1-e^2}.$

Вывод  

Пусть r₁ и r₂ — расстояния до данной точки эллипса от первого и второго фокусов. Пусть также полюс системы координат находится в первом фокусе, а угол $\varphi$ отсчитывается от направления на второй полюс. Тогда, из определения эллипса,

$r_1 + r_2 = 2a.$

Отсюда,

$r_2^2=\left( 2a - r_1 \right)^2 = 4a^2 - 4ar_1 + r_1^2.$

С другой стороны, из теоремы косинусов

$r_2^2 = r_1^2 + 4c^2 - 4r_1c \cos \varphi.$

Исключая $r_2$ из последних двух уравнений, получаем

$r_1 = \frac{a^2-c^2}{a-c \cos \varphi}.$

Учитывая, что

$p = a(1 - e^2),$

получаем искомое уравнение.

Если принять центр эллипса за полюс, а большую ось — за полярную ось, то его уравнение в полярных координатах $\left(\rho, \varphi\right)$ будет иметь вид

$\rho = \frac{b}{\sqrt{1-e^2 \cos^2 \varphi}}.$

Длина дуги эллипса

Длина дуги плоской линии определяется по формуле:

$l = \int \limits_{t_1}^{t_2} \sqrt{\left(\frac{dx}{dt}\right) ^2+\left(\frac{dy}{dt}\right)^2} \,dt.$

Воспользовавшись параметрическим представлением эллипса получаем следующее выражение:

$l = \int \limits_{t_1}^{t_2} \sqrt{a^2 \sin^2 t + b^2 \cos^2 t}\,dt.$

После замены $b^2 = a^2 \left(1 - e^2 \right)$ выражение для длины дуги принимает окончательный вид:

$l = a \int \limits_{t_1}^{t_2} \sqrt{1 - e^2 \cos^2 t}\,dt,\;\;\; e < 1.$

Получившийся интеграл принадлежит семейству эллиптических интегралов, которые в элементарных функциях не выражаются, и сводится к эллиптическому интегралу второго рода $E \left(t,e \right)$. В частности, периметр эллипса равен:

$l = 4a \int \limits_{0}^{\pi/2} \sqrt{1 - e^2 \cos^2 t}\,dt = 4aE(e)$,

где $E \left(e \right)$ — полный эллиптический интеграл второго рода.

Приближённые формулы для периметра

$L=4\frac{\pi ab + (a-b)^2}{a+b}.$

Максимальная погрешность этой формулы ~0,63 % при эксцентриситете эллипса ~0,988 (соотношение осей ~1/6,5). Погрешность всегда положительная.

Приблизительно в два раза меньшие погрешности в широком диапазоне эксцентриситетов дает формула:

$L=4 \cdot \left(a^x+b^x\right)^\left(1/x\right)$, где $x=\frac{\ln 2}{\ln\frac{\pi}{2}}.$

Максимальная погрешность этой формулы ~0,36 % при эксцентриситете эллипса ~0,980 (соотношение осей ~1/5). Погрешность также всегда положительная.

Cущественно лучшую точность при $0,05<a/b<20$ обеспечивает формула Рамануджана:

$L=\pi[3(a+b)-\sqrt{(3a+b)(a+3b)}].$

При эксцентриситете эллипса ~0,980 (соотношение осей ~1/5) погрешность составляет ~0,02 %. Погрешность всегда отрицательная.

Площадь эллипса и его сегмента

Площадь эллипса вычисляется по формуле

$~S = \pi a b.$

Площадь сегмента между дугой, выпуклой влево, и хордой, проходящей через точки $\left(x,\,y\right)$ и $\left(x,\,-y\right):$

$S = \frac{\pi a b}{2} - \frac{b}{a} \left(x\,\sqrt{a^2 - x^2} + a^2 \arcsin \frac{x}{a} \right).$^{[источник не указан 156 дней]}

Если эллипс задан уравнением $A x^2+ B x y + C y^2 = 1$, то площадь можно определить по формуле

$S = \frac{2\pi}{\sqrt{ 4 A C - B^2 }}$.

Построение эллипса

Эллипсограф в действии

Построение с помощью иголок, нитки и карандаша.

Основная статья — статья «Построение эллипса» в Викиучебнике.

Инструментами для рисования эллипса являются:

• эллипсограф;
• две иголки, воткнутые в фокусы эллипса и соединённые ниткой длиной 2a, которую оттягивают карандашом.

При помощи циркуля или циркуля и линейки можно построить любое количество точек, принадлежащих эллипсу, но не весь эллипс целиком.

См. также

• Кривая второго порядка
• Парабола
• Каустика
• Эллипсоид
• Эллипсограф
• Кривая постоянной разности расстояний между двумя точками — гипербола,
• постоянного отношения — окружность Аполлония,
• постоянного произведения — овал Кассини.

Литература

• Корн Г., Корн Т. Свойства окружностей, эллипсов, гипербол и парабол // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 70—73.

Ссылки

	Эллипс в Викисловаре?
	Эллипс на Викискладе?

• А. В. Акопян, А. А. Заславский. Геометрические свойства кривых второго порядка, — М.: МЦНМО, 2007. — 136 с.
• И. Бронштейн. Эллипс // Квант, № 9, 1970.
• А. И. Маркушевич. Замечательные кривые // «Популярные лекции по математике», выпуск 4.
• S.Sykora, Approximations of Ellipse Perimeters and of the Complete Elliptic Integral E(x). Review of known formulae
• Grard P. Michon. Perimeter of an Ellipse (Final Answers), 2000-2005. — 20 c.
• Видео: Как нарисовать эллипс