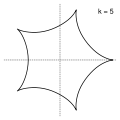
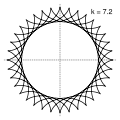
- Гипоциклоида
-
 Красная кривая — гипоциклоида:
Красная кривая — гипоциклоида: ,
,  . Для этой гипоциклоиды
. Для этой гипоциклоиды  .
.Гипоцикло́ида (от греческих слов ὑπό — под, внизу и κύκλος — круг, окружность) — плоская кривая, образуемая точкой окружности, катящейся по внутренней стороне другой окружности без скольжения.
Содержание
Уравнения
где
 , где
, где  — радиус неподвижной окружности,
— радиус неподвижной окружности,  — радиус катящейся окружности.Почему это так
— радиус катящейся окружности.Почему это такПусть в начальный момент окружности касаются в точке А, лежащей на оси OX, где т.О - центр большой окружности. Координаты т.А при этом - (kr, 0), где R/r = k. Рассмотрим, как меняются координаты т.А, привязанной к катящейся окружности (т.А переходит в т.A'). Пусть маленькая окружность прокатилась так, что ее центр перешел из т.C в т.С' и повернулся относительно т.О на угол t. Во-первых, можно показать, что поворот маленькой окружности относительно своего центра при этом (т.е. угол между CA и C'A') равен t - kt = -(k-1)t. Во-вторых, координаты т.C' будут такими: ((k-1)r cos(t), (k-1)r sin(t)). Тогда, зная, куда перейдет центр катящейся окружности, и на какой угол она повернулась относительно этого центра, можно записать координаты т.А':
- x = (k-1)r cos(t) + r cos((k-1)t)
- y = (k-1)t sin(t) - r sin((k-1)t)
Модуль величины
 определяет форму гипоциклоиды. При
определяет форму гипоциклоиды. При  гипоциклоида представляет собой диаметр неподвижной окружности, при
гипоциклоида представляет собой диаметр неподвижной окружности, при  является астроидой.
является астроидой.Пример гипоциклоид
Примечания
См. также
Ссылки
Категории:- Кривые
- Трансцендентные кривые
Wikimedia Foundation. 2010.