- Лемниската Бернулли
-
Лемниска́та Берну́лли — плоская алгебраическая кривая. Определяется как геометрическое место точек, произведение расстояний от которых до двух заданных точек (фокусов) постоянно и равно квадрату половины расстояния между фокусами.
Лемниската по форме напоминает восьмёрку или символ бесконечности.
Содержание
История
Название происходит от греч. λημνισχος — лента, повязка. В Древней Греции «лемнискатой» называли бантик, с помощью которого прикрепляли венок к голове победителя на спортивных играх. Эту лемнискату называют в честь швейцарского математика Якоба Бернулли, положившего начало её изучению.
Уравнение лемнискаты впервые опубликовано в статье Curvatura Laminae Elasticae Якоба Бернулли в журнале Acta eruditorum в 1694 году. Бернулли назвал эту кривую lemniscus и он не знал, что четырнадцатью годами ранее Джованни Кассини уже исследовал более общий случай[1]. Квадратуру лемнискаты впервые выполнил Джюлио-Карло Фаньяно (англ.), опубликовав в 1718 году статью Metodo per misurare la lemniscata и положив тем самым начало изучению эллиптических интегралов, продолженное впоследствии Леонардом Эйлером[2]. Некоторые свойства кривой были также исследованы Якобом Штейнером в 1835 году.
Уравнения
Рассмотрим простейший случай: если расстояние между фокусами
 , расположены они на оси
, расположены они на оси  , и начало координат делит отрезок между ними пополам, то следующие уравнения задают лемнискату:Вывод
, и начало координат делит отрезок между ними пополам, то следующие уравнения задают лемнискату:ВыводФокусы лемнискаты —
 и
и  . Возьмём произвольную точку
. Возьмём произвольную точку  . Произведение расстояний от фокусов до точки
. Произведение расстояний от фокусов до точки  есть
есть ,
,
и по определению оно равно
 :
:Возводим в квадрат обе части равенства:
Раскрываем скобки в левой части:
Раскрываем скобки и свёртываем новый квадрат суммы:
Выносим общий множитель и переносим:
Далее можно сделать замену
 , хотя это не обязательно:
, хотя это не обязательно:В данном случае
 — радиус окружности, описывающей лемнискату.
— радиус окружности, описывающей лемнискату.- Проведя несложные преобразования, можно получить явное уравнение:

ВыводВозводим в квадрат и раскрываем скобки:
Приводим к виду
Это квадратное уравнение относительно
 . Решив его, получим
. Решив его, получимВзяв корень и отбросив вариант с отрицательным вторым слагаемым, получим:
где положительный вариант определяет верхнюю половину лемнискаты, отрицательный — нижнюю.
ВыводИспользуя формулы перехода к полярной системе координат
 получим:
получим:Выносим общие множители и используем тригонометрическое тождество
 :
:Используем ещё одно тождество:
 :
:Делим на
 , предполагая, что
, предполагая, что  :
:Как и в случае прямоугольной системы можно заменить
 :
:- Параметрическое уравнение в прямоугольной системе:
 , где
, где 
Это единственный вариант рациональной параметризации кривой. Уравнение полностью описывает кривую, когда параметр пробегает всю вещественную прямую: от
 до
до  . При этом, когда параметр стремится к
. При этом, когда параметр стремится к  , точка кривой стремится к
, точка кривой стремится к  из второй координатной четверти, а когда параметр стремится к
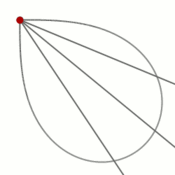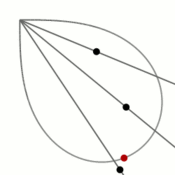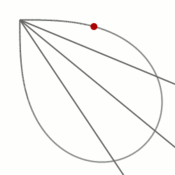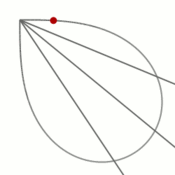
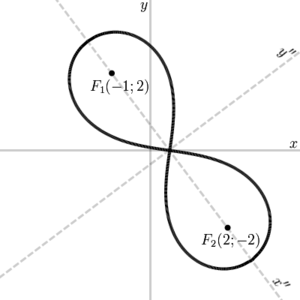
из второй координатной четверти, а когда параметр стремится к  , то — из четвёртой. Распределение точек, которые даёт параметрическое уравнение, при изменении его параметра с фиксированным шагом показано на рисунке.Вывод уравнения
, то — из четвёртой. Распределение точек, которые даёт параметрическое уравнение, при изменении его параметра с фиксированным шагом показано на рисунке.Вывод уравненияУравнение лемнискаты в полярной системе
подставим в формулы перехода к полярной системе координат
 возведённые в квадрат:
возведённые в квадрат:Рассмотрим первое уравнение:
Используем тригонометрические формулы
 и
и  :
:Используем ещё одно легко выводимое тригонометрическое соотношение
 :
:После преобразований:
Извлекаем корень из обеих частей равенства:
Если произвести замену
 , то получаем искомое выражение для
, то получаем искомое выражение для  :
:Второе уравнение выводится аналогично с применением формулы
 .
.Чтобы задать лемнискату по двум произвольным точкам, можно не выводить уравнение заново, а определить преобразование координат, при котором старый (данный) фокусный отрезок переходит в новый, и воздействовать на представленные уравнения этим преобразованием.
ПримерПусть, например,
 — фокусы.
— фокусы.Существует прямоугольная система координат (на рисунке —
 ), в которой уравнение лемнискаты имеет вид
), в которой уравнение лемнискаты имеет видНеобходимо определить преобразование системы координат, переводящее
 в
в  . Это преобразование осуществляется в два этапа: параллельный перенос и поворот.
. Это преобразование осуществляется в два этапа: параллельный перенос и поворот.Середина отрезка
 —
—  , значит перенос только на
, значит перенос только на  по оси
по оси  :
:После переноса системы координат её надо повернуть на некоторый угол. Для определения угла сначала найдём расстояние между фокусами:
значит
 .
.Теперь из геометрических соображений находим синус и косинус угла наклона
 к
к  :
:Формулы преобразования:
Совместив оба преобразования, получим конечные формулы перехода:
Для того, чтобы получить уравнение в стандартной системе координат, подставим эти соотношения в исходное уравнение кривой:
После преобразований:
Это уравнение задаёт лемнискату с фокусами
 в стандартной прямоугольной системе координат.
в стандартной прямоугольной системе координат.Свойства
Лемниската Бернулли является частным случаем овала Кассини при
 , синусоидальной спирали с индексом
, синусоидальной спирали с индексом  и лемнискаты Бута при
и лемнискаты Бута при  , поэтому она наследует некоторые свойства этих кривых.
, поэтому она наследует некоторые свойства этих кривых.Свойства от овала Кассини
- Лемниската — кривая четвёртого порядка.
- Она симметрична относительно двойной точки — середины отрезка между фокусами.
- Кривая имеет 2 максимума и 2 минимума. Их координаты:
- Расстояние от максимума до минимума, находящихся по одну сторону от серединного перпендикуляра отрезка между фокусами равно расстоянию от максимума (или от минимума) до двойной точки.
- Лемнискату описывает окружность радиуса
 , поэтому иногда в уравнениях производят эту замену.
, поэтому иногда в уравнениях производят эту замену.
Свойства от синусоидальной спирали
- Точка, где лемниската пересекает саму себя, называется узловой или двойной точкой.
- Касательные в двойной точке составляют с отрезком
 углы
углы  .
. - Угол
 , составляемый касательной в произвольной точке кривой с радиус-вектором точки касания равен
, составляемый касательной в произвольной точке кривой с радиус-вектором точки касания равен  .
. - Касательные в точках пересечения кривой и хорды, проходящей через двойную точку, параллельны друг другу.
- Инверсия относительно окружности с центром в двойной точке, переводит леминискату Бернулли в равнобочную гиперболу.
- Радиус кривизны лемнискаты есть

Вывод Есть частный случай формулы радиуса кривизны синусоидальной спирали:
 при
при 
однако, легко вывести и по определению.
Уравнение лемнискаты в полярной системе:Формулы перехода к полярной системе координат:
Выражаем
 :
:Подставляем в уравнение лемнискаты и выражаем
 и
и  :
:—- это параметрическое уравнение относительно
 . Проведя некоторые тригонометрические преобразования, можно получить уравнение относительно
. Проведя некоторые тригонометрические преобразования, можно получить уравнение относительно  , указанное выше в разделе Уравнения.
, указанное выше в разделе Уравнения.Формула радиуса кривизны кривой, заданной параметрически:
Находим производные по
 :
:Подставляем в формулу радиуса:
Возвращаемся к уравнению лемнискаты:
Подставляем это выражение в полученную формулу радиуса и получаем:
- Натуральное уравнение кривой имеет вид
- Подерой лемнискаты является синусоидальная спираль
- Лемниската сама является подерой равносторонней гиперболы.
Собственные свойства
- Кривая является геометрическим местом точек, симметричных с центром равносторонней гиперболы относительно её касательных.
- Отрезок биссектрисы угла между фокальными радиусами-векторами точки лемнискаты равен отрезку от центра лемнискаты до пересечения её оси с этой биссектрисой.
- Материальная точка, движущаяся по кривой под действием однородного гравитационного поля, пробегает дугу за то же время, что и соответствующую хорду. При этом ось лемнискаты составляет угол
 с вектором напряжённости поля, а центр лемнискаты совпадает с исходным положением движущейся точки.
с вектором напряжённости поля, а центр лемнискаты совпадает с исходным положением движущейся точки. - Площадь полярного сектора
![\varphi\in[0,\alpha]](d9de782030822a97ffd502b173282d6c.png) , при
, при  :
:
- В частности, площадь каждой петли
 , то есть площадь, ограниченная кривой, равна площади квадрата со стороной
, то есть площадь, ограниченная кривой, равна площади квадрата со стороной  .
.
- Перпендикуляр, опущенный из фокуса лемнискаты на радиус-вектор какой-либо её точки, делит площадь соответствующего сектора пополам.
- Длина дуги лемнискаты между точками
 и
и  выражается эллиптическим интегралом I рода:
выражается эллиптическим интегралом I рода:
 где
где 
- В частности, длина всей лемнискаты
Построения
При помощи секущих (способ Маклорена)
Строится окружность радиуса
 с центром в одном из фокусов. Из середины
с центром в одном из фокусов. Из середины  фокусного отрезка строится произвольная секущая
фокусного отрезка строится произвольная секущая  (
( и
и  — точки пересечения с окружностью), и на ней в обе стороны откладываются отрезки
— точки пересечения с окружностью), и на ней в обе стороны откладываются отрезки  и
и  , равные хорде
, равные хорде  . Точки
. Точки  ,
,  лежат на разных петлях лемнискаты.
лежат на разных петлях лемнискаты.Шарнирные методы
Вариант первый
На плоскости выбираются две точки —
 и
и  — будущие фокусы лемнискаты. Собирается специальная конструкция из трёх скреплённых в ряд на шарнирах отрезков, чтобы полученная линия могла свободно изгибаться в двух местах (точки сгиба —
— будущие фокусы лемнискаты. Собирается специальная конструкция из трёх скреплённых в ряд на шарнирах отрезков, чтобы полученная линия могла свободно изгибаться в двух местах (точки сгиба —  и
и  ). При этом необходимо соблюсти пропорции отрезков:
). При этом необходимо соблюсти пропорции отрезков:  . Края линии крепятся к фокусам. При непараллельном вращении отрезков вокруг фокусов середина центрального отрезка опишет лемнискату Бернулли.
. Края линии крепятся к фокусам. При непараллельном вращении отрезков вокруг фокусов середина центрального отрезка опишет лемнискату Бернулли.Вариант второй
В этом варианте лемниската строится по фокусу и двойной точке —
 и
и  соответственно. Собирается почти такая же шарнирная конструкция как и в предыдущем варианте, но прикреплённый к двойной точке отрезок
соответственно. Собирается почти такая же шарнирная конструкция как и в предыдущем варианте, но прикреплённый к двойной точке отрезок  соединяется не с концом центрального
соединяется не с концом центрального  , а с его серединой. Пропорции также другие:
, а с его серединой. Пропорции также другие:  .
.-
Механизм Ватта (анимация)
См. также
- Лемниската — общий случай с несколькими фокусами
- Овал Кассини — обобщение на произведение расстояний до фокусов
- Синусоидальная спираль — обобщение по виду параметрического уравнения
- Лемниската Бута
- Плоская кривая
- Алгебраическая кривая
- Бесконечность
- Аттрактор Лоренца
Примечания
- ↑ Статья об Овалах Кассини на сайте о плоских кривых (англ.). Архивировано из первоисточника 22 августа 2011. Проверено 15 июня 2010.
- ↑ Bradley R. E., D'Antonio L. A., Sandifer C. E. Euler at 300: an appreciation. — P. 121-123.
Литература
- Математическая энциклопедия (в 5-и томах). — М.: Советская Энциклопедия, 1982.
- Маркушевич А. И. Замечательные кривые. — Популярные лекции по математике. — М.: Гостехиздат, 1952. — С. 23-25.
- Савелов А. А. Плоские кривые / Под. ред. А. П. Нордена. — М.: ФИЗМАТГИЗ, 1960. — С. 155-162.
- Lockwood E. H. A book of curves. — Cambridge: Cambridge university press, 1961. — P. 110-117.
Ссылки
- Статья на сайте Wolfram MathWorld (англ.). Проверено 15 июня 2010.
- Статья в Encyclopédie des Formes Mathématiques Remarquables (фр.). Архивировано из первоисточника 22 августа 2011. Проверено 15 июня 2010.
- Фаньяно и длина дуги лемнискаты (итал.). Архивировано из первоисточника 22 августа 2011. Проверено 15 июня 2010.
Категории:- Алгебраические кривые
- Кривые
Wikimedia Foundation. 2010.



































 , где
, где  — биссектриса
— биссектриса  ;
; для любой точки кривой;
для любой точки кривой;