- Теорема косинусов
-
Теорема косинусов — теорема евклидовой геометрии, обобщающая теорему Пифагора:
Для плоского треугольника со сторонами
 и углом
и углом  , противолежащим стороне
, противолежащим стороне  , справедливо соотношение:
, справедливо соотношение: .
.
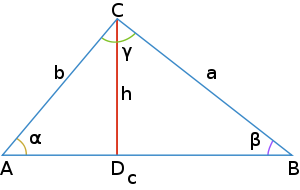
Класcическое доказательствоРассмотрим треугольник ABC. Из вершины C на сторону AB опущена высота CD. Из треугольника ADC следует:
 ,
,
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
Приравниваем правые части уравнений (1) и (2) и:
или
 .
.
Случай, когда один из углов при основании тупой (и высота падает на продолжение основания), полностью аналогичен рассмотренному.
Выражения для сторон b и c:

 .
.
Доказательство через координатыОдно из самых красивых и простых доказательств теоремы косинусов является доказательство её в координатной плоскости.
Внесём в координатную плоскость произвольный треугольник ABC так, чтобы точка А совпала с началом координат, а прямая АВ лежала на прямой ОХ. Введём обозначения AB=c,AC=b,CB=a, a угол CAB=α(пока будем считать что α≠90°).
Тогда точка A имеет координаты (0;0), точка B(c;0). Через функцию sin и cos, а также сторону АС=b выведем координаты точки С. С(b×cosα;b×sinα). Координаты точки С остаются неизменными при тупом и остром угле α.
Зная координаты С и B, а также зная, что CB=a, найдя длину отрезка, мы можем составить равенство:



Так как
 (основное тригонометрическое тождество), то
(основное тригонометрическое тождество), то

Теорема доказана.
Стоит отметить, что для прямого угла α, теорема также работает cos90°=0 и a²=b²+с² - известная всем теорема Пифагора. Но так как в основе координатного метода лежит теорема Пифагора, то доказательство её через теорему косинусов не совсем правильно.Содержание
Следствие из теоремы косинусов
Следствие теоремы косинусов опирается на свойства функции cos:
- Если
 , то cosα>0
, то cosα>0 - Ecли α=90°, то cosα=0
- Если
 , то cosα<0
, то cosα<0
Теперь из полученной ранее формулы выразим соsα:



 , при любых b и c (так как это положительные длины сторон), значит:
, при любых b и c (так как это положительные длины сторон), значит:- Если
 , угол α — острый
, угол α — острый - Если
 , угол α — прямой
, угол α — прямой - Если
 , угол α — тупой
, угол α — тупой
История
Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов, были сформулированы отдельно для случаев острого и тупого угла в 12 и 13 предложениях II книги «Начал» Евклида.
Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях математиков стран Средней Азии. Теорему косинусов для сферического треугольника в привычном нам виде сформулировал Региомонтан, назвав её «теоремой Альбатегния» (по имени ал-Баттани).
В Европе теорему косинусов популяризовал Франсуа Виет в XVI столетии. В начале XIX столетия её стали записывать в принятых по сей день алгебраических обозначениях.
Вариации и обобщения
- Теоремы косинусов (сферическая геометрия) или Теорема косинусов для трехгранного угла.
- Теоремы косинусов (геометрия Лобачевского)
Четырёхугольник
Возводя в квадрат тождество
 можно получить утверждение, иногда называемое теоремой косинусов для четырёхугольников:
можно получить утверждение, иногда называемое теоремой косинусов для четырёхугольников: , где
, где  — угол между прямыми AB и CD.
— угол между прямыми AB и CD.
Или иначе:
Симплекс
при этом мы должны зачеркнуть строку и столбец, где находится
 или
или  .
.A — угол между гранями
 и
и  ,
,  -грань, находящаяся против вершины i ,
-грань, находящаяся против вершины i , - расстояние между вершинами i и j.
- расстояние между вершинами i и j.См. также
- Решение треугольников
- Скалярное произведение
- Соотношение Бретшнайдера
- Теорема косинусов для трехгранного угла
- Сферическая теорема косинусов
- Теорема котангенсов
- Теорема синусов
- Теорема тангенсов
Литература
- Понарин Я. П. Элементарная геометрия. В 2 тт. — М.: МЦНМО, 2004. — С. 84-85. — ISBN 5-94057-170-0
Категории:- Теоремы
- Геометрия треугольника
- Тригонометрия
Wikimedia Foundation. 2010.