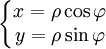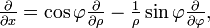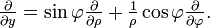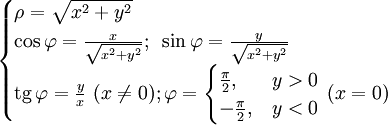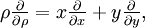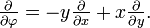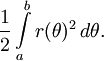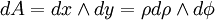Полярные координаты

Полярная система координат — система координат, ставящая в соответствие каждой точке на плоскости пару чисел $~(\rho; \varphi)$.

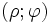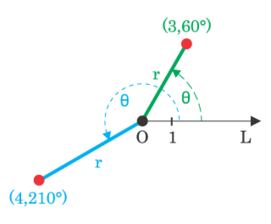
Основными понятиями этой системы являются точка отсчёта (полюс) и луч, начинающийся в этой точке (полярная ось).

Координата ρ определяет расстояние от точки до полюса, координата $\varphi$ — угол между полярной осью и отрезком, соединяющим полюс и рассматриваемую точку. Координата $\varphi$ берётся со знаком «+», если угол от оси до отрезка вычисляется против часовой стрелки, и со знаком «-» в противоположном случае. 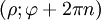Любая точка в этой системе имеет бесконечное число координат вида $(\rho; \varphi+ 2\pi n)$, которым соответствует одна и та же точка при любых натуральных 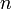$~n$. Для полюса ρ = 0, а угол 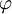$\varphi~$ произвольный.

Иногда допускаются отрицательные значения ρ, в этом случае координаты (ρ,φ) и ( − ρ,φ + π) определяют одну и ту же точку плоскости.

Примеры использования

• Уравнение прямой на расстоянии D от полюса: ρ = D / cos(φ + α)
• Уравнение окружности с центром в полюсе и радиуса R: ρ = R
• Уравнение окружности, проходящей через полюс и радиуса R: ρ = 2Rcos(φ + α)
• Уравнение эллипса с фокусом в полюсе: $\rho = \frac{p}{1-e \cdot \cos \phi}$

Формулы перехода

• от полярной системы координат к декартовой:
  

  $\left\{\begin{matrix} x=\rho\cos\varphi~\\ y=\rho\sin\varphi~\end{matrix}\right.$
  

  $\tfrac{\partial}{\partial x}= \cos\varphi \tfrac{\partial}{\partial \rho} - \tfrac 1{\rho} \sin\varphi \tfrac{\partial}{\partial \varphi} ,$
  

  $\tfrac{\partial}{\partial y} = \sin\varphi \tfrac{\partial}{\partial \rho} + \tfrac 1{\rho} \cos\varphi \tfrac{\partial}{\partial \varphi} .$
  

• от декартовой системы координат к полярной:
  

  $\begin{cases} \rho=\sqrt{x^2+y^2}~ \\ \cos\varphi=\frac{x}{\sqrt{x^2+y^2}};~\sin\varphi=\frac{y}{\sqrt{x^2+y^2}}~\\ \mathop{\mathrm{tg}}\,\varphi=\frac{y}{x} \ (x \ne 0); \varphi=\begin{cases}{\pi\over 2}, & y>0\\-{\pi\over 2}, & y<0 \end{cases} \ (x=0) \end{cases}$
  

  $\rho\tfrac{\partial}{\partial \rho}= x \tfrac{\partial}{\partial x} + y \tfrac{\partial}{\partial y} ,$
  

  $\tfrac{\partial}{\partial \varphi} = -y \tfrac{\partial}{\partial x} + x \tfrac{\partial}{\partial y} .$
  

Свойства

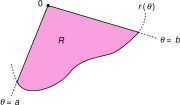Область интегрирования R заключена между кривой ρ(φ) и лучами начинающиеся из начала координат с полярными углами φ = a φ = b.

• Обозначим область интегрирования R между кривой ρ(φ) и лучами φ = a φ = b, где 0 < b − a < 2π. Тогда площадь R записывается в виде определённого интеграла

  $\frac12\int\limits_a^b r(\theta)^2\, d\theta.$

• Элемент площади в полярной системе координат имеет вид

  $dA=dx\wedge dy=\rho d\rho\wedge d\phi$

  • В частости, для произвольной функции f(ρ,φ), имеет место формула

    $\iint\limits_R f(\rho,\phi) dA = \int\limits_a^b \int\limits_0^{\rho(\phi)} f(\rho,\phi)\rho d\rho d\phi,$
    .

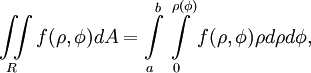
См. также

Ссылки