- Ортодромия
-
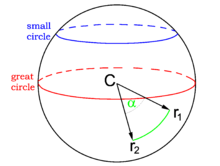
 Ортодрома делит сферу на две полусферы
Ортодрома делит сферу на две полусферы
Ортодромия, ортодрома (из др.-греч. ὀρθός «прямой» + δρόμος «бег, путь») — кратчайшая линия между двумя точками на поверхности вращения. В картографии и навигации — название геодезической линии кратчайшего расстояния между двумя точками на поверхности земного шара, наименьший из отрезков дуги большого круга, проходящей через эти точки. В отличие от локсодромии ортодромия пересекает меридианы под разными углами. В судо- и самолётовождении, где Земля принимается за шар, ортодромия представляет собой дугу большого круга.
Экватор и меридианы являются частными случаями ортодромии. Через две точки на земной поверхности, расположенные не на противоположных концах одного диаметра Земли, можно провести только одну ортодромию.
В большинстве картографических проекций ортодромии изображаются кривыми линиями (за исключением, быть может, меридианов и экватора). Это неудобно для прокладки кратчайших маршрутов. В гномонической проекции все ортодромии изображены прямыми линиями.
Параллели (за исключением экватора) не являются ортодромиями.
Содержание
Расчёт ортодромии
Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей.Длина, начальный и конечный азимуты, широты промежуточных точек ортодромии рассчитываются по следующим формулам (выводятся с помощью соотношений сферической тригонометрии)[1].
Длина ортодромии: D= 111,12 * arccos(sinφ1 * sinφ2 + cosφ1 * cosφ2 * cos(λ2 — λ1)).
Начальный азимут: ctgα1 = cosφ1 tgφ2 / sin(λ2 — λ1) — sinφ1 / tg(λ2 — λ1).
Конечный азимут: ctgα2 = sinφ2 / tg(λ2 — λ1) — cosφ2 tgφ1 / sin(λ2 — λ1).
Широта промежуточной точки: φ = arctg((tgφ1 * sin(λ2 — λ)/sin(λ2 — λ1)) + (tgφ2 * sin(λ — λ1) / sin(λ2 — λ1)).
Обозначения: D — длина ортодромии, φ1 — широта точки отбытия, λ1 — долгота точки отбытия, φ2 — широта точки прибытия, λ2 — долгота точки прибытия, φ — широта промежуточной точки, λ — долгота произвольно взятой промежуточной точки ортодромии, 111,12 — длина дуги 1° меридиана (может быть выбрана иная величина).
Для примера возьмём перелёт из Внукова (координаты: 55°35′46″ с. ш., 37°16′03″в. д.) в Пулково (координаты: 59°48′01″ с. ш., 30°15′45″в. д.).
В десятичном выражении координаты точек отбытия и прибытия выглядят так: 55,596111, 37,2675 и 59,8002778, 30,2625. Длина дуги 1° меридиана — 111,3 км.
Находим длину ортодромии: sin55,596111 * sin59,8002778 + cos55,596111 * cos59,8002778 * cos(30,2625 — 37,2675) = 0,825075 * 0,864277 + 0,565023 * 0,5030158 * 0,9925355 = 0,71309335 + 0,282094 = 0,99518735. acos0,99518735 = 5,62346633. 5,62346633 * 111,3 = 625,892 км.
Находим начальный азимут: cos55,596111 tg59,8002778 / sin(30,2625 — 37,2675) — sin55,596111 / tg(30,2625 — 37,2675) = 0,565023 * 1,7181812 / (-0,121956)- 0,825075 / (-0,122873) = −7,9603455 + 6,71486 = −1,2454855. −1,2454855−1 = −0,80289975. tg(-0,80289975) = −38,761° = 321,239°.
Находим конечный азимут: sin59,8002778 / tg(30,2625 — 37,2675) — cos59,8002778 * tg55,596111 / sin(30,2625 — 37,2675) = 0,864277 / (-0,122873) — 0,5030158 * 1,4602505 / (-0,121956) = −7,033905 — (-6,024605) = −1,0093. −1,0093−1 = −0,990786. atg(-0,990786) = −44,73481 = 315,2652° или 315°15′55″.
В геометрии
В геометрии ортодромия — кратчайшая линия между двумя точками на поверхности вращения.
См. также
Примечания
- ↑ Михайлов В.С., Кудрявцев В.Г., Давыдов В.С. 26.2. Основные формулы ортодромии. Способы ее задания // Навигация и лоция. — Киев, 2009.
Ссылки
Категории:- Геодезия
- Картография
Wikimedia Foundation. 2010.