Плоскость (геометрия)

У этого термина существуют и другие значения, см. Плоскость.

Сюда перенаправляется запрос «Плоскостность». На эту тему нужна отдельная статья.

Две пересекающиеся плоскости

Пло́скость — одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии.

Некоторые характеристические свойства плоскости

• Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки;
• Две плоскости являются либо параллельными, либо пересекаются по прямой.
• Прямая либо параллельна плоскости, либо пересекает ее в одной точке, либо находится на плоскости.
• Две прямые, перпендикулярные одной и той же плоскости, параллельны друг другу.
• Две плоскости, перпендикулярные одной и той же прямой, параллельны друг другу.

Аналогично отрезку и интервалу, плоскость, не включающую крайние точки, можно назвать интервальной плоскостью, или открытой плоскостью.

Плоскость и два её нормальных вектора: n₁ и n₂

Уравнения плоскости

Впервые встречается у А. К. Клеро (1731).

Уравнение плоскости в отрезках, по-видимому, впервые встречается у Г.Ламе (1816—1818).

Нормальное уравнение ввёл Л. О. Гессе (1861).

Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.

• Общее уравнение (полное) плоскости

$Ax+By+Cz+D=0\qquad (1)$

где $~A,B,C$ и $~D$ — постоянные, причём $~A,B$ и $~C$ одновременно не равны нулю; в векторной форме:

$(\mathbf{r},\mathbf{N})+D=0$

где $\mathbf{r}$ — радиус-вектор точки $~M(x,y,z)$, вектор $\mathbf{N}=(A,B,C)$ перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора $\mathbf{N}$:

$\cos \alpha = \frac{A}{\sqrt{A^2+B^2+C^2}},$

$\cos \beta = \frac{B}{\sqrt{A^2+B^2+C^2}},$

$\cos \gamma = \frac{C}{\sqrt{A^2+B^2+C^2}}.$

Если один из коэффициентов в уравнении плоскости равен нулю, уравнение называется неполным. При $~D=0$ плоскость проходит через начало координат, при $~A=0$ (или $~B=0$, $~C=0$) П. параллельна оси $~Ox$ (соответственно $~Oy$ или $~Oz$). При $~A=B=0$ ($~A=C=0$, или $~B=C=0$) плоскость параллельна плоскости $~Oxy$ (соответственно $~Oxz$ или $~Oyz$).

• Уравнение плоскости в отрезках:

$\frac{x}{a}+ \frac{y}{b}+ \frac{z}{c}=1,$

где $~a=-D/A$, $~b=-D/B$, $~c=-D/C$ — отрезки, отсекаемые плоскостью на осях $~Ox, Oy$ и $~Oz$.

• Уравнение плоскости, проходящей через точку $~M(x_0,y_0,z_0)$ перпендикулярно вектору нормали $\mathbf{N}(A,B,C)$:

$~A(x-x_0)+B(y-y_0)+C(z-z_0)=0;$

в векторной форме:

$((\mathbf{r}-\mathbf{r_0}),\mathbf{N})=0.$

• Уравнение плоскости, проходящей через три заданные точки $~M(x_i,y_i,z_i)$, не лежащие на одной прямой:

$((\mathbf{r}-\mathbf{r_1}),(\mathbf{r_2}-\mathbf{r_1}),(\mathbf{r_3}-\mathbf{r_1}))=0$

(смешанное произведение векторов), иначе

$\left| \begin{matrix}x-x_1&y-y_1&z-z_1\\ x_2-x_1&y_2-y_1&z_2-z_1\\ x_3-x_1&y_3-y_1&z_3-z_1\\ \end{matrix}\right|=0.$

• Нормальное (нормированное) уравнение плоскости

$x \cos \alpha+ y \cos \beta+ z \cos \gamma - p=0 \qquad (2)$

в векторной форме:

$(\mathbf{r},\mathbf{N^0})\mathbf{-p}=0,$

где $\mathbf{N^0}$- единичный вектор, $~p$ — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель

$\mu = \pm \frac{1}{\sqrt{A^2+B^2+C^2}}$

(знаки $~\mu$ и $~D$ противоположны).

Определение по точке и вектору нормали

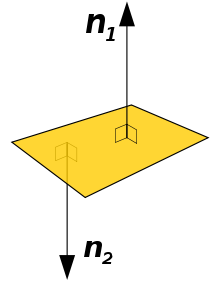
В трехмерном пространстве одним из важнейших способов определения плоскости является указание точки на плоскости и вектора нормали к ней.

Допустим, $r_0$ является радиусом-вектором точки $P_0$, заданной на плоскости, и допустим, что n - это ненулевой вектор, перпендикулярный к плоскости (нормаль). Идея состоит в том, что точка $P$ с радиусом-вектором r находится на плоскости тогда и только тогда, когда вектор, проведённый от $P_0$ к $P$, перпендикулярен n.

Вернёмся к тому, что два вектора являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю. Отсюда следует, что нужная нам плоскость может быть выражена как множество всех точек r таких, что:

$\bold n\cdot (\bold r-\bold r_0)=0.$ (Здесь точка означает скалярное произведение, а не умножение.)

Развернув выражение, мы получим:

$n_x (x-x_0)+ n_y(y-y_0)+ n_z(z-z_0)=0,\,$

что является знакомым нам уравнением плоскости.

Например: Дано: точка на плоскости $P(2,6,-3)$ и вектор нормали $N(9,5,2)$.

Уравнение плоскости записывается так:

$9(x - 2) + 5(y - 6) + 2(z + 3) = 0$

$-18 + 9x -30 + 5y + 6 + 2z = 0$

$9x + 5y + 2z - 42 = 0$

Расстояние от точки до плоскости

Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.

• Отклонение точки $~M_1(x_1,y_1,z_1)$ от плоскости заданной нормированным уравнением $~(2)$

$~\delta = x_1 \cos \alpha + y_1 \cos \beta + z_1 \cos \gamma - p;$

$~\delta>0$,если $~M_1$ и начало координат лежат по разные стороны плоскости, в противоположном случае $~\delta<0$. Расстояние от точки до плоскости равно $~|\delta|.$

• Расстояние $~\rho$ от точки $~M_0(x_0, y_0, z_0)$, до плоскости, заданной уравнением $~ax+by+cz+d=0$, вычисляется по формуле:

$\rho = \frac{\mid ax_0+by_0+cz_0+d\mid}{\sqrt{a^2+b^2+c^2}}$

Расстояние между параллельными плоскостями

• Расстояние между плоскостями, заданными уравнениями $~Ax+By+Cz+D_1=0$ и $~Ax+By+Cz+D_2=0$:

$d=\frac{\mid D_2-D_1\mid}{\sqrt{A^2+B^2+C^2}}$

• Расстояние между плоскостями, заданными уравнениями $\bar n (\bar r - \bar{r_1})=0$ и $\bar n (\bar r - \bar{r_2})=0$:

$d=\frac{\mid[\bar r_2 - \bar r_1, \bar n]\mid}{\mid\bar n\mid}$

Типы взаимного расположения трёх или менее плоскостей. В частности, 4 тип — пересечение двух плоскостей, 11 тип — плоскость E₃ проходит через линию пересечения плоскостей E₁ и E₂, 12 тип — пересечение трёх плоскостей в точке

Связанные понятия

• Угол между двумя плоскостями. Если уравнения П. заданы в виде (1), то

$\cos \varphi = \frac{A_1A_2+B_1B_2+C_1C_2}{\sqrt{(A_1^2+B_1^2+C_1^2) (A_2^2+B_2^2+C_2^2)}};$

Если в векторной форме, то

$\cos \varphi = \frac{(\mathbf{N_1}, \mathbf{N_2})}{|\mathbf{N_1}||\mathbf{N_2}|}.$

• Плоскости параллельны, если

$\frac{A_1}{A_2}=\frac{B_1}{B_2}=\frac{C_1}{C_2}$ или $[\mathbf{N_1}, \mathbf{N_2}]=0.$ (Векторное произведение)

• Плоскости перпендикулярны, если

$~A_1A_2+B_1B_2+C_1C_2=0$ или $(\mathbf{N_1}, \mathbf{N_2})=0$. (Скалярное произведение)

• Пучок плоскостей — все плоскости, проходящие через линию пересечения двух плоскостей. Уравнение пучка плоскостей, то есть любой плоскости, проходящей через линию пересечения двух плоскостей, имеет вид^[1]:222:

$~\alpha(A_1x+B_1y+C_1z+D_1)+\beta(A_2x+B_2y+C_2z+D_2)=0,$

где $\alpha$ и $\beta$ — любые числа, не равные одновременно нулю. Уравнение самой этой линии можно найти из уравнения пучка, подставляя α=1, β=0 и α=0, β=1.

• Связка плоскостей — все плоскости, проходящие через точку пересечения трёх плоскостей^[1]:224. Уравнение связки плоскостей, то есть любой плоскости, проходящей через точку пересечения трёх плоскостей, имеет вид:

$~\alpha(A_1x+B_1y+C_1z+D_1)+\beta(A_2x+B_2y+C_2z+D_2)+\gamma(A_3x+B_3y+C_3z+D_3)=0,$

где $\alpha$, $\beta$ и $\gamma$ — любые числа, не равные одновременно нулю. Саму эту точку можно найти из уравнения связки, подставляя α=1, β=0, γ=0; α=0, β=1, γ=0 и α=0, β=0, γ=1 и решая получившуюся систему уравнений.

N-плоскость в пространстве $R^n$

Пусть дано n-мерное аффинный-точененое пространство $K^n(V,P)$, над полем действительных чисел. В нём выбрана прямоугольная система координат $O, \vec{e_1},...,\vec{e_n}$. m-плоскостью называется множество точек $\alpha$, радиус векторы которых удовлетворяют следующему соотношению $\alpha = \{x| x = A_{nm}\vec{t_m} + \vec{d}\}.$ $A_{nm}$ - матрица, столбцы которой образует направляющие подпространство плоскости, $\vec{t}$ - вектор переменных, $\vec{d}$ - радиус-вектор одной из точек плоскости.
Указанное соотношение можно из матрично-векторного вида перевести в векторный:
$x = \vec{a_1}t_1 + ... + \vec{a_m}t_m + d, \vec{a_i} \in V$ - векторное уравнение m-плоскости.
Вектора $\vec{a_i}$ образуют направляющее подпространство. Две m-плоскости $\alpha, \beta$ называются параллельными, если их направляющие пространства совпадают и $\exists x \in \alpha : x \notin \beta$.

(n-1)-плоскость в n-мерном пространстве называется гиперплоскостью или просто плоскостью. Для гиперплоскости существует общее уравнение плоскости. Пусть $\vec{n}$ - нормальный вектор плоскости, $\vec{r} = (x^1,...,x^n)$ - вектор переменных, $\vec{r_0}$ - радиус вектор точки, принадлежащей плоскости, тогда:
$(\vec{r} - \vec{r_0}, \vec{n}) = 0$ - общее уравнение плоскости.
Имя матрицу направляющих векторов, уравнение можно записать так: $det(\vec{r} - \vec{r_0} | A_{n,n-1}) = 0$, или:
$\begin{vmatrix} x^1 - x_{0}^1 & a_{1}^1 & a_{2}^1 & ... & a_{n-1}^1 \\ x^2 - x_{0}^2 & a_{1}^2 & a_{2}^1 & ... & a_{n-1}^2 \\ ... & ... & ... & ... \\ x^n - x_{0}^n & a_{1}^n & a_{2}^n & ... & a_{n-1}^n \end{vmatrix} = 0$.
Углом между плоскостями называется наименьший угол между их нормальными векторами.

Примеры m-плоскостей

1. Примером 1-плоскости в трёхмерном пространстве (n=3) служит прямая. Её векторное уравнение имеет вид: $\alpha = \{a_x,a_y,a_z\}t + \{b_x,b_y,b_z\}$. В случае n = 2 прямая является гиперплоскостью.
2. Гиперплоскостью в трёхмерном пространстве соответствует привычному понятию плоскости.

См. также

• Прямая
• Сагиттальная плоскость
• Полуплоскость
• Пространство

Примечания

1. ↑ ^{1 2} Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах. — М.: Высшая школа, 1985. — 232 с.

Литература

Ильин В. А., Позняк Э. Г. Аналитическая геометрия. — М.: ФИЗМАТЛИТ, 2002. — 240 с.

Ссылки

• На Викискладе есть медиафайлы по теме Плоскость (геометрия)