- Окружность Аполлония
-
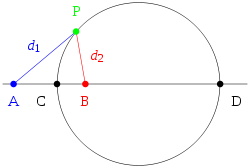
Окружность Аполло́ния — геометрическое место точек плоскости, отношение расстояний от которых до двух заданных точек — величина постоянная, не равная единице.
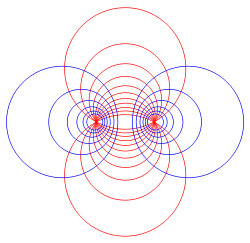
Биполярные координаты — ортогональная система координат на плоскости, основанная на кругах Аполлония.
Пусть на плоскости даны две точки
 и
и  . Рассмотрим все точки
. Рассмотрим все точки  этой плоскости, для каждой из которых
этой плоскости, для каждой из которых ,
,
где
 — фиксированное положительное число. При
— фиксированное положительное число. При  эти точки заполняют срединный перпендикуляр к отрезку
эти точки заполняют срединный перпендикуляр к отрезку  ; в остальных случаях указанное геометрическое место — окружность, называемая окружностью Аполлония.
; в остальных случаях указанное геометрическое место — окружность, называемая окружностью Аполлония.Кривая постоянной разности расстояний между двумя точками — гипербола, постоянной суммы — эллипс, постоянного произведения — овал Кассини.
Содержание
Свойства
- Радиус окружности Аполлония равен

- Отрезок
 между точкой на окружности и точкой пересечения ее с прямой
между точкой на окружности и точкой пересечения ее с прямой  является биссектрисой самого угла
является биссектрисой самого угла  или угла, смежного с ним.
или угла, смежного с ним. - Центр данной окружности лежит на прямой, соединяющей эти две точки.
Приложения
- Одно из решений задачи Брахмагупты основано на построении окружности Аполония.
- Окружность Аполлония находит применение при решении задачи сближения на плоскости с использованием стратегии параллельного сближения.
См. также
Примечания
 Категория:
Категория:- Евклидова геометрия
Wikimedia Foundation. 2010.