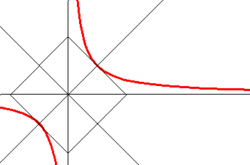
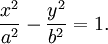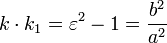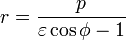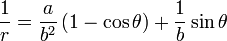- Равнобочная гипербола
-
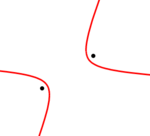 Гипербола и её фокусы
Гипербола и её фокусыГипе́рбола — геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F1 и F2 (называемых фокусами) постоянно, то есть
- | | F1M | − | F2M | | = C
Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, большим единицы.
Термин «гипербола» (греч. ύπερβολή — избыток) был введён Аполлонием Пергским, поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком.
Каноническое уравнение гиперболы
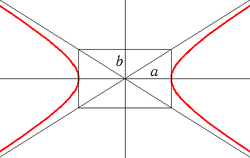 Гипербола, её полуоси и асимптоты
Гипербола, её полуоси и асимптотыДля любой гиперболы можно найти декартову систему координат такую, что гипербола будет описываться уравнением:
Числа
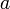 и
и 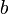 называются соответственно вещественной и мнимой полуосями гиперболы.
называются соответственно вещественной и мнимой полуосями гиперболы.Асимптотика
Каждая гипербола имеет пару асимптот:
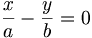 и
и 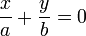 .
.
Связанные определения
- Осью гиперболы называется прямая, соединяющая её фокусы.
- Расстояние от начала координат до одного из фокусов гиперболы называют фокусным расстоянием гиперболы
 .
. - Расстояние от начала координат до одной из вершин гиперболы называется большой или вещественной полуосью гиперболы
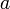 .
. - Расстояние от вершины гиперболы до асимптоты вдоль направления параллельного оси ординат называется малой или мнимой полуосью гиперболы
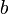 .
. - Отношение фокусного расстояния к большой полуоси гиперболы называется эксцентриситетом:
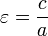 . Эксцентриситет гиперболы всегда больше единицы.
. Эксцентриситет гиперболы всегда больше единицы. - Расстояние от фокуса до гиперболы вдоль прямой, параллельной оси ординат называется фокальным параметром
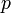 ..
.. - В задачах, связанных с движением тел по гиперболическим траекториям расстояние от фокуса до ближайшей вершины гиперболы называется перицентрическим расстоянием
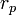 .
. - Прицельным параметром называется расстояние от фокуса до одной из асимптот гиперболы. Прицельный параметр равен малой полуоси гиперболы.
Соотношения между элементами гиперболы
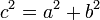 .
.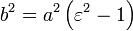 .
.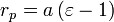 .
.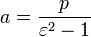 .
.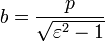 .
.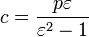 .
.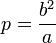 .
.
Диаметры гиперболы
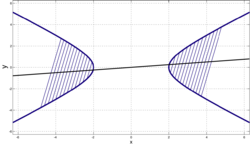 Диаметры гиперболы
Диаметры гиперболыДиаметром гиперболы, как и всякого конического сечения, является прямая, проходящая через середины параллельных хорд. Каждому направлению параллельных хорд соответствует свой сопряженный диаметр. Все диаметры гиперболы проходят через её центр. Диаметр, соответствующий хордам, параллельным мнимой оси, есть действительная ось; диаметр соответствующий хордам, параллельным действительной оси, есть мнимая ось.
Угловой коэффициент
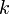 параллельных хорд и угловой коэффициент
параллельных хорд и угловой коэффициент 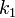 соответствующего диаметра связан соотношением
соответствующего диаметра связан соотношениемЕсли диаметр a делит пополам хорды, параллельные диаметру b, то диаметр b делит пополам хорды, параллельные диаметру a. Такие диаметры называются взаимно сопряженными. Главными диаметрами называются взимно сопряженные и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.
Уравнение гиперболы в полярных координатах
Если полюс находится в фокусе гиперболы, а вершина гиперболы лежит на продолжении полярной оси, то
Если полюс находится в фокусе гиперболы, а полярная ось параллельна одной из асимптот, то
Равнобочная гипербола
Гиперболу, у которой a = b, называют равнобочной. Равнобочная гипербола в некоторой прямоугольной системе координат описывается уравнением
- xy = a2 / 2.
Примером равнобочной гиперболы служит график функции y = 1 / x.
Гиперболы, связанные с треугольником
- гипербола Енжабека — кривая, изогонально сопряженная прямой Эйлера;
- гипербола Киперта — кривая, изогонально сопряженная прямой OK, где K — Точка Лемуана, а O — центр описанной окружности данного треугольника.
Оптические свойства гиперболы
Свет от источника, находящегося в одном из фокусов гиперболы, отражается второй ветвью гиперболы таким образом, что продолжения отраженных лучей пересекаются во втором фокусе.
См. также
Литература
- Бронштейн И. Гипербола // Квант. — 1975. — № 3.
- Математическая энциклопедия (в 5-и томах). М.: Советская энциклопедия, 1982.
- Маркушевич А. И. Замечательные кривые // Популярные лекции по математике. — Гостехиздат, 1952. — В. 4.
Конические сечения Главные типы Эллипс • Гипербола • Парабола Вырожденные Точка • Прямая • Пара прямых Частный случай эллипса Окружность Геометрическое построение Коническое сечение • Шары Данделена Математика • Геометрия
Wikimedia Foundation. 2010.