- Тригонометрические тождества
-
Тригонометрические тождества — математические выражения для тригонометрических функций, которые выполняются при всех значениях аргумента (из общей области определения).
Основные тригонометрические формулы
Формула Допустимые значения аргумента Номер 

(1) 

(2) 

(3) Формула (1) является следствием теоремы Пифагора. Формулы (2) и (3) получаются из формулы (1) делением на
 и
и  соответственно.
соответственно.Формулы сложения аргументов
Формулы сложения аргументов 
(4) 
(5) 
(6) 
(7) Формула (6) получается при делении (4) на (5). А формула (7) — при делении (5) на (4)
Вывод формул
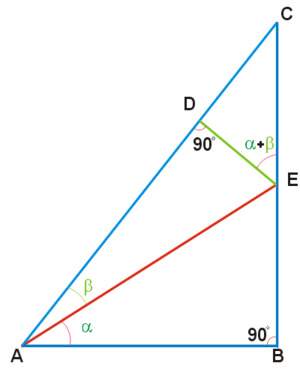
На Рис. 4 изображены четыре прямоугольных треугольника: ABC, ABE, ADE и CDE.
Принято, что AE = 1,
 .
.Так как AE = 1, то



 .
.
Из треугольника ABC следует:
Из треугольника CDE следует:
 .
.
Приравниваем правые части уравнений (14) и (16):
Приравниваем правые части уравнений (15) и (17) и решаем, полученное уравнение относительно CE:

 .
.
Подставляем (CE) из (19) в (18):
 .
.
Полученное значение для CD подставляем в (15):





 .
.
Итак:
 .
.
Из формулы (15) следует:
Из формулы (16) и (17) следует:
Приравниваем правые части (21) и (22) и находим
 :
:Подставляем значение
 :
:Итак:
 .
.
Формулы двойного угла
Формулы двойного угла выводятся из формул (4), (5) , (6) и (7), если принять, что угол β равен углу α:
Формулы двойного угла 
(23) 

(24) 
(25)  Примечания
Примечаниядля формулы
 :
:для формулы
 :
: 
Формулы тройного угла
Формулы тройного угла 


 Примечания
Примечаниядля формулы
 :
: 
для формулы :
:  ;
;Формулы понижения степени
Формулы понижения степени выводятся из формул (24):
Синус Косинус Произведение 
(26) 
(27) 









Формулы преобразования произведений функций
Формулы преобразования произведений функций 
(28) 
(29) 
(30) Вывод формул преобразования произведений функцийФормулы сложения функций выводятся из формул сложения аргументов (5), (6) и (7). Например, из формулы (5) следует:

 .
.
То есть:
 — формула (29).
— формула (29).
Остальные формулы преобразования произведений функций выводятся аналогично.
Формулы преобразования суммы функций
Формулы преобразования суммы функций 
(31) 
(32) 
(33) 
(34) 
(35) Вывод формул преобразования суммы функцийФормулы преобразования суммы функций выводятся из формул преобразования произведений функций (28), (29), (30) и (31) с помощью подстановки:
и
 .
.
Подставим эти выражения в формулу (28):
 , то есть
, то есть — формула (33).
— формула (33).
Остальные формулы преобразования суммы синуса и косинуса выводятся аналогично. Из формулы (6) следует:


 , то есть
, то есть — формула (34).
— формула (34).
Преобразование суммы синусов 3-x разных углов в произведение при :
 :
:Решение простых тригонометрических уравнений
-
- Если
 — вещественных решений нет.
— вещественных решений нет. - Если
 — решением является число вида
— решением является число вида 
- Если
-
- Если
 — решений нет.
— решений нет. - Если
 — решением является число вида
— решением является число вида 
- Если
-
- Решением является число вида

- Решением является число вида
-
- Решением является число вида

- Решением является число вида
Универсальная тригонометрическая подстановка
Тождества имеют смысл, только когда существуют обе части (то есть при
 ).
).





Вспомогательный аргумент (формулы сложения гармонических колебаний)


Полезные тождества














Представление тригонометрических функций в комплексной форме
Формула Эйлера утверждает, что для любого вещественного числа
 выполнено следующее равенство:
выполнено следующее равенство:где
 — основание натурального логарифма,
— основание натурального логарифма,При помощи формулы Эйлера можно определить функции
 и
и  следующим образом:
следующим образом: ,
, .
.
Откуда:
См. также
Категория:- Тригонометрия
Wikimedia Foundation. 2010.





















 —
— 


