- Индекс ветвления
-
Кривая Урысона (далее кривая) — наиболее общее (но не чрезмерно) определение кривой, введённое Урысоном в 1921. Это определение обобщает определение Кантора на произвольную размерность. Определение формулируется следующим образом:
Кривой называется связное компактное топологическое пространство C топологической размерности 1.
Определение кривой Урысона является внутренним: оно характеризуется лишь свойствами самого пространства C и не зависит от того, рассматривается ли это пространство само по себе или как подмножество другого топологического пространства.
Существуют кривые, которые не гомеоморфны никакому подмножеству плоскости. Такова, например, кривая, лежащая в трёхмерном пространстве и состоящая из шести рёбер тетраэдра и четырёх отрезков, соединяющих центр тетраэдра с его вершинами. Но всякая кривая гомеоморфна некоторому подмножеству трёхмерного евклидова пространства (теорема Менгера). Более того, существует кривая M, обладающая тем свойством, что, какова бы ни была кривая C, в M найдется подмножество C', гомеоморфное C. Это трёхмерный аналог ковра Серпинского, называемый губкой Менгера.
Содержание
Индекс ветвления
В исследовании кривых важную роль играет понятие индекса ветвления. Кривая C в точке x имеет индекс ветвления α, если α есть минимальное кардинальное число такое, что для любой окрестности x существует меньшая окрестность, граница которой есть множество мощности, не превосходящей α. Точка кривой C, индекс ветвления которой больше двух, называется точкой ветвления; точка, индекс ветвления которой равен единице, называется концевой точкой.
Точки кривой относительно их индекса ветвления классифицируются следующим образом.
- Точки с индексом ветвления n, где n ― натуральное число.
- Точки неограниченного индекса ветвления. (Точка x кривой C имеет неограниченный индекс ветвления, если для любой окрестности x, существует меньшая окрестность, граница которой состоит из конечного множества точек; но при этом индекс ветвления бесконечен.)
- Точки счётного индекса ветвления.
- Точки континуального индекса ветвления.
Примеры
- Отрезок во всех своих внутренних точках имеет индекс ветвления, равный двум; индекс ветвления концов отрезка равен единице.
- Окружность в каждой своей точке имеет индекс ветвления два.
- Кривая, состоящая из n прямолинейных отрезков, исходящих из одной точки O, имеет в точке O индекс ветвления n.
- Кривая, состоящая из отрезков
 выходящих из начала координат O, имеющих длины
выходящих из начала координат O, имеющих длины 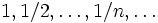 и исходящие из O под углами
и исходящие из O под углами 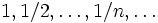 к оси OX имеет неограниченный индекс ветвления в O
к оси OX имеет неограниченный индекс ветвления в O
- Если при этом сделать все отрезки равной длины, то O будет иметь счетный индекс ветвления.
- Кривая, состоящая из отрезков, соединяющих точку O со всеми точками канторова множества, лежащего на другом отрезке, имеет во всех своих точках континуальный индекс ветвления с.
- Ковер Серпинского также имеет во всех своих точках континуальный индекс ветвления.
- Салфетка Серпинского представляет пример кривой состоящий только из точек с индексом ветвления 2, 3 и 4.
- При этом индекс ветвления 2 имеют только вершины основного треугольника. В частности если склеить две салфетки Серпинского по вершинам основного треугольника получим кривую с индексами ветвления 3 и 4.
Свойства
- Если у кривой совсем нет точек ветвления, то есть если в каждой точке кривой индекс ветвления равен 1 или 2, то эта кривая есть либо простая дуга ― топологический образ отрезка, либо простая замкнутая линия ― топологический образ окружности.
- При этом, если индекс ветвления кривой во всех точках равен 2, то это ― простая замкнутая кривая, если же у кривой, не имеющей точек ветвления, есть концевые точки (при этом оказывается, что их непременно две), то она будет простой дугой.
- Если кривая имеет лишь конечное число точек ветвления, причем индекс ветвления каждой из них также конечен, то такая кривая может быть разбита на конечное число простых дуг, не имеющих попарно никаких других общих точек, кроме своих концов.
- Окружность является единственной кривой, все точки которой имеют один и тот же конечный индекс ветвления 2; других кривых, имеющих во всех точках один и тот же конечный индекс ветвления, нет. Более того,
- Если все точки кривой L имеют индекс ветвления больший или равный n, то на L найдется точка, индекс ветвления которой больше или равен 2n − 2, и при всяком натуральном n существует кривая, состоящая только из точек, имеющих индекс ветвления n и 2n − 2 (теорема Урысона).
Литература
- Урысон П. С. Труды по топологии и другим областям математики, т. 2, — М.― Л., 1951;
Wikimedia Foundation. 2010.
