КРУГОВОЕ ПОЛЕ

поле деления круг а,- поле получающееся присоединением к полю рациональных чисел первообразного корня 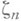из единицы степени га, где п - некоторое натуральное число. Иногда (локальным) круговым полем наз. также поле вида 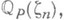где 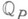- поле рациональных р-адических чисел. Так как при нечетном n, обычно предполагается, что Тогда различным n соответствуют неизоморфные поля К _п.

К. п. естественно возникают в задаче о делении круга - деление окружности на n равных частей эквивалентно построению на комплексной плоскости первообразного корня К. п, устроены "достаточно просто", и поэтому дают удобный экспериментальный материал для создания общих понятий теории чисел. Напр., понятие целого алгебраич. числа и дивизора возникли первоначально при рассмотрении К. п.

Место К. п. среди всех полей алгебраич. чисел выясняет теорема Кронекера - Вебера, утверждающая, что конечное расширение абелево тогда и только тогда, когда для нек-рого п. Аналогичное утверждение выполняется и для локальных К. п.

Алгебраическая теория. Поле К _п является абелевым расширением поля 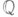с группой Галуа где 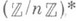- мультипликативная группа кольца вычетов по модулю га. В частности, степень равна 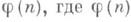- функция Эйлера. Поле К _п чисто мнимое и имеет степень 2 над своим максимальным вполне вещественным подполем 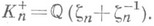Если - разложение пна простые множители,

то К _п является свободным композитом полей . В поле 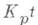простой дивизор римеет индекс ветвления 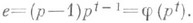В .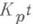 имеет место равенство главных дивизоров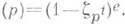

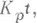Все остальные простые дивизоры поля неразветвлены в . откуда следует, что рразветвлен в поле . тогда и только тогда, когда

Числа образуют фундаментальный базис поля К _n. Дискриминант поля 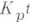равен 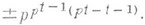Для линейно разделенных над полей Еи Fсо взаимно простыми дискриминантами выполняется соотношение Это позволяет вычислить для произвольного га (см. [3]). Для поля числа вида

где 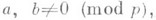порождают подгруппу конечного индекса в группе всех единиц. Элементы этой подгруппы наз. круговыми единицами.

Закон разложения для К. п., т. е. закон, по к-рому простые дивизоры (р).поля разлагаются в произведение простых дивизоров в 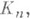- частный случай общего закона разложения в абелевых расширениях, доставляемого теорией полей классов (см. [4]). А именно, если ( р, n)=1 и f - наименьшее натуральное число, для к-рого то в К _n 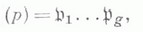где простые дивизоры попарно различны, . Таким образом, тип разложения (р).зависит только от вычета р(mod n). В случае, когда точный вид разложения (р).можно получить, учитывая, что где (т, р)=1 и (р) вполне разветвлен в

Если К - максимальное абелево расширение то и

где 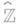- пополнение кольца целых чисел 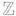по всем идеалам конечного индекса. В частности, для любого простого lсуществует единственное расширение 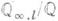с группой Галуа, изоморфной группе целых l-адических чисел

Согласно теории полей классов существует отображение взаимности

где - группа иделей поля В случае К. п. отображение 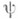допускает простое и явное описание (см. [4]). Аналитическая теория. Многие результаты о строении группы классов дивизоров поля К _п удается получить с помощью аналитпч. методов. Если h _п - число классов поля К _п, то

где w, D и R - число корней из единицы, дискриминант и регулятор поля 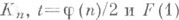- некоторая явно вычислимая константа, 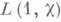- L-функция Дирихле, соответствующая характеру , где пробегает все нетривиальные мультипликативные характеры mod n. В свою очередь, для существуют явные выражения в терминах гауссовых сумм (см. [7] гл. 5). Этим решается вопрос о вычислении при заданном п.

Существует естественное разложение на два множителя - первый и второй множители числа классов, причем интерпретируется как число классов поля 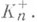В случае, когда где Е - группа единиц поля 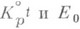- группа круговых единиц (любая круговая единица становится действительной после умножения на подходящий корень из единицы).

Для задач, связанных с проблемой Ферма, важную роль играет вдпрос о делимости числа классов поля К _l на lдля простых l. Известно, что 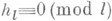для бесконечного числа простых l(такие lназ. иррегулярными). Относительно регулярных простых чисел l, т. е. чисел, для к-рых 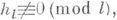до сих пор не известно (1982), конечно или бесконечно их число. Существует гипотеза, что 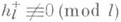для всех l. Эта гипотеза проверена для большого числа примеров. Легче поддается исследованию множитель 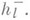Существует относительно простой критерий делимости 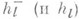на lв терминах чисел Бернулли [7]. Известно, что 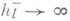при и что 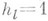тогда и только тогда, когда 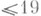(см. [6]).

Для исследования группы классов К. п. успешно применяются так наз. р-адические L-функции (см. [5], [8]).

Лит.:[1] К u m m е г Е., "J. reine und angew. Math.", 1847, Bd 35, S. 327-67; [2] В е й л ь Г., Алгебраическая теория чисел, пер. с англ., М., 1947; [3] Л енг С., Алгебраические числа, пер. с. англ., М., 1966; [4] Алгебраическая теория чисел, пер. с англ., М., 1969; [5] Ш а ф а р е в и ч И. Р., Дзета-функция, М., 1969; [6] U с h i d а К., "Tohoku Math. J.", 1971, V, 23, р, 573-80; [7] Б о р е в и ч 3. И., Ш а ф а р е в и ч И. Р., Теория чисел, 2 изд., М., 1972; [8] Iwasawa К., Lectures on p-adic L-functions, N. Y. - Tokyo, 1972; [9] bang S., Cyclotomic fields, Priceton.- Hdlb.- В., 1978. Л. В. Кузьмин.