- ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ
- функция вида

где z= (z1, ..., zn) - комплексные или действительные переменные, aj, b, с j, d- комплексные или действительные коэффициенты, |с 1| + ... + | с n| + |d|>0. Если |с 1| = .. .= |с п| = 0, то Д.-л. ф. является целой линейной функцией; если ранг матрицы.
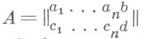 равен единице, то L(z)- постоянная
равен единице, то L(z)- постояннаяСобственно Д.-л. ф. получается, если |c1|+ .. . + |cn| >0 и ранг Аравен двум; ниже эти условия предполагаются выполненными.
В случае n=1 и действительных a1=а, с 1=с, z1 = z график Д.-л. ф. есть равнобочная гипербола с асимптотами z=-d/c и w=a/c. В случае ге=2 и действительных a1, а 2, b,c1, c2, d, z1, z2 график Д.-л. ф. есть гиперболич. параболоид.
В случае n=1 Д.-л. ф. L(z)есть аналитич. функция комплексного переменного zвсюду в расширенной комплексной плоскости С, за исключением точки z=-d/c, в к-рой L(z)имеет простой полюс. При n>1 Д.-л. ф. L(z) есть мероморфная функция в пространстве С n комплексных переменных z=(zl,..., zn), имеющая полярным множеством множество

См. также Дробно-линейное отображение.
Е. П. Долженко, Е. Д. Соломенцев
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
