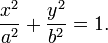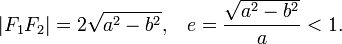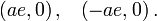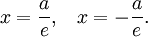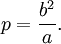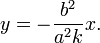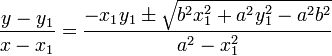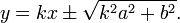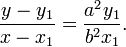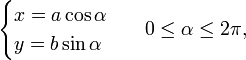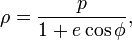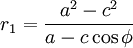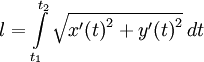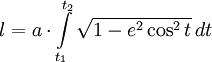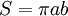- Эллипс (геометрич.)
-
- Не следует путать с термином «Эллипсис».
 Эллипс и его фокусы
Эллипс и его фокусыЭ́ллипс (др.-греч. ἔλλειψις — недостаток, в смысле недостатка эксцентриситета до 1) — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний от двух данных точек F1 и F2 (называемых фокусами) постоянна, то есть
- | F1M | + | F2M | = 2a.
Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой. Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.
Содержание
Связанные определения
- Отрезок AB, проходящий через фокусы эллипса, концы которого лежат на эллипсе, называется большой осью данного эллипса. Длина большой оси равна 2a в вышеприведённом уравнении.
- Отрезок CD, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса.
- Точка пересечения большой и малой осей эллипса называется его центром.
- Точка пересечения эллипса с осями называются его вершинами.
- Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса, и обозначаются a и b.
- Расстояния r1 и r2 от каждого из фокусов до данной точки на эллипсе называются фокальными радиусами в этой точке.
- Расстояние
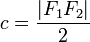 называется фокальным расстоянием.
называется фокальным расстоянием. - Эксцентриситетом эллипса называется отношение
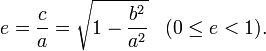 . Эксцентриситет (также обозначается ε) характеризует вытянутость эллипса изменяется. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
. Эксцентриситет (также обозначается ε) характеризует вытянутость эллипса изменяется. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут. - Фокальным параметром
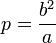 называется половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса.
называется половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса. - Отношение длин малой и большой полуосей называется коэффициентом сжатия эллипса или эллиптичностью:
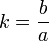 . Величина, равная
. Величина, равная 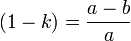 называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент и эксцентриситет эллипса связаны соотношением
называется сжатием эллипса. Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент и эксцентриситет эллипса связаны соотношением 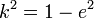
Свойства
- Фокальное свойство. Если F1 и F2 — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой (F1X) равен углу между этой касательной и прямой (F2X).
- Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
- Эволютой эллипса является астроида.
Эллипс также можно описать как
- фигуру, которую можно получить из окружности, применяя аффинное преобразование
- ортогональную проекцию окружности на плоскость.
- Пересечение плоскости и кругового цилиндра
Соотношения между элементами эллипса
 Части эллипса (описание см. в разделе "Связанные определения")
Части эллипса (описание см. в разделе "Связанные определения")- Малая полуось:
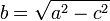 ;
; - Расстояние от фокуса до ближней вершины:
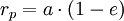 ;
; - Расстояние от фокуса до дальней вершины:
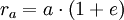 ;
; - Связь фокального параметра с полуосями и фокусным расстоянием:
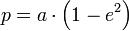 ;
;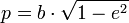 ;
;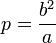 ;
;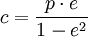 ;
;
- Связь фокального параметра с удалением вершин от данного фокуса:
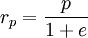 ;
;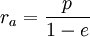 ;
;
Координатное представление
Каноническое уравнение
Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):
Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат. Для определённости положим, что
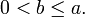 В этом случае величины a' и b — соответственно, большая и малая полуоси эллипса.
В этом случае величины a' и b — соответственно, большая и малая полуоси эллипса.Зная полуоси эллипса можно вычислить его фокальное расстояние и эксцентриситет:
Координаты фокусов эллипса:
Эллипс имеет две директриссы, уравнения которых можно записать как
Фокальный параметр (т.е. половина длины хорды, проходящей через фокус и перпендикулярной оси эллипса) равен
Уравнение диаметра, сопряжённого хордам с угловым коэффициентом k:
Уравнение касательных, проходящих через точку
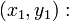
Уравнение касательных, имеющих данный угловой коэффициент k::
Уравнение нормали в точке
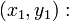
Параметрическое уравнение
Каноническое уравнение эллипса может быть параметризовано:
где
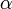 — параметр уравнения.
— параметр уравнения.Уравнение в полярных координатах
Если принять фокус эллипса за полюс, а ось — за полярную ось, то его уравнение в полярных координатах
 будет иметь вид
будет иметь видгде e — эксцентриситет, а p — фокальный параметр.
ВыводПусть r1 и r2 расстояния до данной точки эллипса из первого и второго фокусов. Пусть, также полюс системы координат находится в первом фокусе, а угол φ отсчитывается от направления на второй полюс. Тогда, из определения эллипса,
- r1 + r2 = 2a.
Отсюда,
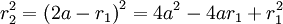 .
.
С другой стороны, из теоремы косинусов
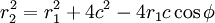 .
.
Исключая r2 из последних двух уравнений, получаем
Учитывая, что
- p = a(1 − e2),
получаем искомое уравнение.
Другое уравнение в полярных координатах:
Длина дуги эллипса
Длина дуги плоской линии определяется по формуле:
Воспользовавшись параметрическим представлением эллипса получаем следующее выражение:
Получившийся интеграл принадлежит семейству эллиптических интегралов, которые в элементарных функциях не выражаются, и сводится к эллипическому интегралу второго рода
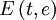 . В частности, периметр эллипса равен:
. В частности, периметр эллипса равен: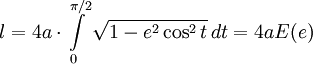 ,
,
где
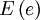 — полный эллиптический интеграл второго рода.
— полный эллиптический интеграл второго рода.Приближённые формулы для периметра
YNOT:
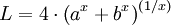 где
где 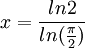 Максимальная погрешность этой формулы ~0.3619 % при эксцентриситете эллипса ~0.979811 (соотношение осей ~1/5). Погрешность всегда положительная.
Максимальная погрешность этой формулы ~0.3619 % при эксцентриситете эллипса ~0.979811 (соотношение осей ~1/5). Погрешность всегда положительная.Очень приближенная формула
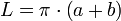
Площадь эллипса
Площадь эллипса вычисляется по формуле
где
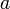 и
и  полуоси эллипса.
полуоси эллипса.Построение эллипса
Пусть даны две взаимноперпендикулярные прямые (оси будущего эллипса) и два отрезка длиной a (большая полуось) и b (малая полуось). Точку пересечения прямых обозначим как O, это центр эллипса.
C помощью циркуля
- Раствором циркуля, равным a, с центром в точке O отметим на одной из прямой точки P1 и Р2, а на второй прямой раствором, равным b — точки Q1 и Q2. Полученные точки являются вершинами эллипса, а отрезки P1Р2 и Q1Q2 — его большая и малая оси, соответственно.
- Раствором циркуля, равным a, с центром в точке Q1 (или Q2) отметим на отрезке P1Р2 точки F1 и F2. Полученные точки являются фокусами эллипса.
- На отрезке P1Р2 выберем произвольную точку T. Затем с помощью циркуля начертим две окружности: первую — радуса, равным длине отрезка TP1, с центром в точке F1 и вторую радуса, равным длине отрезка TP2, с центром в точке F2. Точки пересечения этих окружностей принадлежат искомому эллипсу, т.к. сумма расстояний из обоих фокусов равна длине большой оси 2a.
- Повторяя необходимое число раз шаги предыдущего пункта, получим искомый эллипс.
C помощью циркуля и линейки
- Раствором циркуля, равным a, с центром в точке O отметим на одной из прямой точки P1 и Р2, а на второй прямой раствором, равным b — точки Q1 и Q2. Полученные точки являются вершинами эллипса, а отрезки P1Р2 и Q1Q2 — его большая и малая оси, соответственно.
- С помощью линейки проводим через точку O произвольную наклонную линию. Затем раствором циркуля, равным а, с центром в точке O отмечаем на ней точку S, а раствором, равным b — точку R.
- Затем из точки S опускаем перепендикуляр на прямую P1Р2. Для этого произвольным раствором циркуля (но бо́льшим, чем расстояние от точки до прямой), с центром в точке S отмечаем на отрезке P1Р2 две точки, переносим в них циркуль и отмечаем тем же радиусом точку персечения окружностей S. Затем с помощью линейки соединяем точки S и S, это и есть искомый перпендикуляр.
- Аналогичным способом опускаем перепендикуляр из точки R на прямую Q1Q2.
- Точка пересечения построенных перпендикуляров принадлежит эллипсу.
- Повторяя необходимое число раз шаги четырёх предыдущих пунктов, получим искомый эллипс.
Ссылки
- А. В. Акопян, А. А. Заславский Геометрические свойства кривых второго порядка, — М.: МЦНМО, 2007. — 136 с.
- И. Бронштейн, Эллипс, Квант, № 9, 1970.
- А. И. Маркушевич.Замечательные кривые «Популярные лекции по математике». Выпуск 04.
См. также
Конические сечения Главные типы Эллипс • Гипербола • Парабола Вырожденные Точка • Прямая • Пара прямых Частный случай эллипса Окружность Геометрическое построение Коническое сечение • Шары Данделена Математика • Геометрия
Wikimedia Foundation. 2010.