Линия Коха

Кривая Коха

Кривая Коха — фрактальная кривая, описанная в 1904 году шведским математиком Хельге фон Кохом. Кривая Коха примечательна тем, что нигде не имеет касательной, т. е. нигде не дифференцируема, хотя всюду непрерывна.

Три копии кривой Коха, построенные (остриями наружу) на сторонах правильного треугольника, образуют замкнутую кривую, называемую снежинкой Коха.

Построение

Кривая Коха является типичным геометрическим фракталом. Процесс её построения выглядит следующим образом: берём единичный отрезок, разделяем на три равные части и заменяем средний интервал равносторонним треугольником без этого сегмента. В результате образуется ломаная, состоящая из четырех звеньев длины 1/3. На следующем шаге повторяем операцию для каждого из четырёх получившихся звеньев и т. д… Предельная кривая и есть кривая Коха.

Свойства

• Кривая Коха нигде не дифференцируема и не спрямляема.
• Кривая Коха не имеет самопересечений.
• Кривая Коха имеет промежуточную (т. е. не целую) хаусдорфову размерность, которая равна 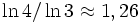$\ln4/\ln3\approx 1,26$ поскольку она состоит из четырёх равных частей, каждая из которых подобна всей кривой с коэффициентом подобия 1/3.

Обобщения

Возможны обобщения кривой Коха, также использующие при построении подстановку ломаной из четырёх равных отрезков, но имеющей иную геометрию. Они имеют хаусдорфову размерность от 1 до 2. В частности, если вместо деления отрезка 1:1:1 использовать золотое сечение (φ:1:φ), то получившаяся кривая имеет отношение к мозаикам Пенроуза.

Также, можно построить кривую «Крест Коха» на сторонах квадрата, при этом проводя построение «внутрь» квадрата.

Так же можно построить "Снежинку Коха" на сторонах равностороннего трегоугольника.