Хаусдорфова размерность

Размерность Хаусдорфа — естественный способ определить размерность множества в метрическом пространстве. Размерность Хаусдорфа согласуется с нашими обычными представлениями о размерности в тех случаях, когда эти обычные представления есть. Например, в трёхмерном евклидовом пространстве хаусдорфова размерность конечного множества равна нулю, размерность гладкой кривой — единице, размерность гладкой поверхности — двум и размерность множества ненулевого объёма — трём. Для фрактальных множеств размерность Хаусдорфа может принимать дробные значения.

Определение

Определение размерности Хаусдорфа непросто и состоит из нескольких шагов. Пусть Ω — ограниченное множество в метрическом пространстве X.

$\varepsilon$-покрытия

Пусть 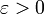$\varepsilon>0$. Не более чем счётный набор 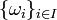$\{\omega_i\}_{i\in I}$ подмножеств пространства X будем называть $\varepsilon$-покрытием множества Ω, если выполнены следующие два свойства:

• $\Omega \subset \bigcup_{i\in I}\omega_i$
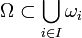
• для любого 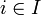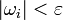$i\in I$: $|\omega_i|<\varepsilon$ (здесь и далее | ω | означает диаметр множества ω).

α-мера Хаусдорфа

Пусть α > 0. Пусть 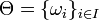$\Theta=\{\omega_i\}_{i\in I}$ — покрытие множества Ω. Определим следующую функцию, в некотором смысле показывающую «размер» этого покрытия: $F_\alpha(\Theta):=\sum\limits_{i\in I} |\omega_i|^\alpha$.

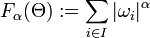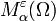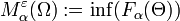Обозначим через $M^{\varepsilon}_{\alpha}(\Omega)$ «минимальный размер» ${\varepsilon}$-покрытия множества Ω: $M^{\varepsilon}_{\alpha}(\Omega) := \inf(F_\alpha(\Theta))$, где инфимум берётся по всем $\varepsilon$-покрытиям множества Ω.

Очевидно, что функция 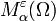$M^{\varepsilon}_{\alpha}(\Omega)$ (нестрого) возрастает при уменьшении $\varepsilon$, поскольку при уменьшении $\varepsilon$ мы только сжимаем множество возможных $\varepsilon$-покрытий. Следовательно, у неё есть конечный или бесконечный предел при $\varepsilon\rightarrow 0+$:

$M_{\alpha}(\Omega)=\lim\limits_{\varepsilon\rightarrow 0+}M^{\varepsilon}_{\alpha}(\Omega)$.

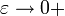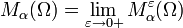Величина M_α(Ω) называется α-мерой Хаусдорфа множества Ω.

Свойства α-меры Хаусдорфа

• α-мера Хаусдорфа является борелевской мерой на X.
• с точностью до умножения на коэффициент: 1-мера Хаусдорфа для гладких кривых совпадает с их длиной; 2-мера Хаусдорфа для гладких поверхностей совпадает с их площадью; d-мера Хаусдорфа множеств в 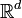$\mathbb{R}^d$ совпадает с их d-мерным объёмом.
• M_α(Ω) убывает по α. Более того, для любого множества Ω существует критическое значение α₀, такое, что:
  • M_α(Ω) = 0 для всех α > α₀
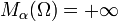  • $M_{\alpha}(\Omega)=+\infty$ для всех α < α₀

Значение 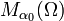$M_{\alpha_0}(\Omega)$ может быть нулевым, конечным положительным или бесконечным.

Определение размерности Хаусдорфа

Размерностью Хаусдорфа множества Ω называется число α₀ из предыдущего пункта.

Свойства размерности Хаусдорфа

• Размерность Хаусдорфа любого множества не превосходит нижней и верхней размерностей Минковского.
• Размерность Хаусдорфа не более чем счётного объединения множеств равна макcимуму из их размерностей. В частности, добавление счётного множества к любому множеству не меняет его размерности.
• Для самоподобных множеств размерность Хаусдорфа может быть вычислена явно. Неформально говоря, если множество разбивается на n частей, подобных исходному множеству с коэффициентами 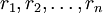$r_1,r_2,\dots,r_n$, то его размерность s является решением уравнения 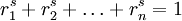$r_1^s+r_2^s+\dots+r_n^s = 1$. Например, размерность множества Кантора равна ln2 / ln3 (разбивается на две части, коэффициент подобия 1/3), а размерность треугольника Серпинского — ln3 / ln2 (разбивается на 3 части, коэффициент подобия 1/2).

См. также

• фрактал
• размерность Минковского

Литература

• Федер Е. Фракталы. — М.: МИР, 1991. — С. 254. — ISBN 5-03-001712-7