Квадрат

Это статья о геометрической фигуре. Другие значения слова см. на странице Квадрат (значения)

Квадрат
Рёбра	4
Символ Шлефли	{4}
Вид симметрии	Диэдрическая группа (D4)
Площадь	t2
Внутренний угол (градусы)	90°

Квадра́т — правильный четырёхугольник, у которого все углы и стороны равны.

Квадрат

Признаки квадрата

1) Равенство длин сторон; 2) Равенство углов (по 90 градусов)

Свойства

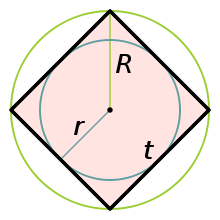
• Пусть $t$ — сторона квадрата, $R$ — радиус описанной окружности, $r$ — радиус вписанной окружности. Тогда центр описанной и вписанной окружностей квадрата совпадает с точкой пересечения его диагоналей, и
  • радиус вписанной окружности квадрата равен половине стороны квадрата:

    $r = \frac{t}{2}$,

  • радиус описанной окружности квадрата равен половине диагонали квадрата:

    $R = \frac{\sqrt 2}{2} t$,

  • периметр квадрата равен:

    $P = 4 t = 4 \sqrt 2 R = 8 r$,

  • площадь $S$ равна

    $S = t^2 = 2 R^2 = 4 r^2$.

• Квадрат обладает наибольшей симметрией среди всех четырёхугольников. Он имеет
  • одну ось симметрии четвёртого порядка (ось, перпендикулярная плоскости квадрата и проходящая через его центр);
  • четыре оси симметрии второго порядка (что для плоской фигуры эквивалентно отражениям), из которых две проходят вдоль диагоналей квадрата, а другие две — параллельно сторонам.
• Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Площадь квадрата и длина его сторон

Линии симметрии

Построение квадрата с использованием циркуля и линейки

Неевклидова геометрия

В неевклидовой геометрии квадрат (более широко) - многоугольник с четырьмя равными сторонами и равными углами.

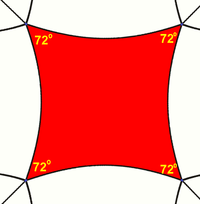
Многообразие квадратов

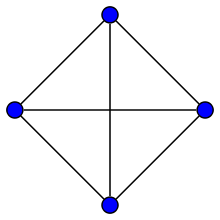
Графы: K₄ полный граф часто изображается как квадрат с 6 рёбрами.

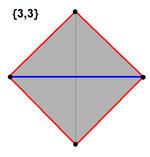
3-симплекс (3D)

• Флаг Лима
  

  Флаг Лима, будучи поднятым на корабле в гавани, означает, что корабль находится на карантине
• Шахматная доска

Интересное

В виде квадратиков иногда отображаются некоторые символы по причине сложного начертания. Например:឴឴្ឳឲឣបឫឹី៛ݮݯݲݼݳݴඝඟඟදශණඪයරතඡඣ

См. также

• Квадратом называют возведение в степень 2
• Квадратура круга
• Квадрирование квадрата
• Единичный квадрат
• Marching squares

Примечания

Ссылки

	Фото на Викискладе?

• Квадрат, геометрическая фигура // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.). — СПб., 1890—1907.