Призма (геометрия)

У этого термина существуют и другие значения, см. Призма.

	призма в Викисловаре?
	Category:Prisms (geometry) на Викискладе?

Призма (от др.-греч. πρίσμα (лат. prisma) «нечто отпиленное») — многогранник, две грани которого являются конгруэнтными (равными) многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Или (равносильно) — это многогранник, в основаниях которого лежат равные многоугольники, а боковые грани — параллелограммы.

Призма является разновидностью цилиндра (в общем смысле).

Элементы призмы

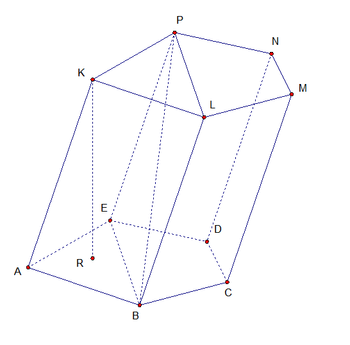
Название	Определение	Обозначения на чертеже	Чертеж
Основания	Две грани, являющиеся конгруэнтными многоугольниками, лежащими в параллельных плоскостях.	$ABCDE$, $KLMNP$
Боковые грани	Все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом.	$ABLK$, $BCML$, $CDNM$, $DEPN$, $EAKP$
Боковая поверхность	Объединение боковых граней.
Полная поверхность	Объединение оснований и боковой поверхности.
Боковые ребра	Общие стороны боковых граней.	$AK$, $BL$, $CM$, $DN$, $EP$
Высота	Отрезок, соединяющий основания призмы и перпендикулярный им.	$KR$
Диагональ	Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.	$BP$
Диагональная плоскость	Плоскость, проходящая через боковое ребро призмы и диагональ основания.
Диагональное сечение	Пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе его частные случаи — ромб, прямоугольник, квадрат.	$EBLP$
Перпендикулярное сечение	Пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Свойства призмы

• Основания призмы являются равными многоугольниками.
• Боковые грани призмы являются параллелограммами.
• Боковые ребра призмы параллельны и равны.
• Объём призмы равен произведению её высоты на площадь основания:

$V=S\cdot h$

• Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
• Площадь боковой поверхности произвольной призмы $S=P\cdot l$, где $P$ — периметр перпендикулярного сечения, $l$ — длина бокового ребра.
• Площадь боковой поверхности правильной призмы $S=P\cdot h$, где $P$ — периметр основания призмы, , $h$ — высота призмы.
• Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы.
• Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих боковых рёбрах.
• Перпендикулярное сечение перпендикулярно ко всем боковым граням.

Виды призм

Призма, основанием которой является параллелограмм, называется параллелепипедом.

Прямая призма - это призма, у которой боковые ребра перпендикулярны плоскости основания. Другие призмы называются наклонными.

Правильная призма - это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы - равные прямоугольники.

Правильная призма, боковые грани которой являются квадратами (высота которой равна стороне основания), является полуправильным многогранником.

См. также

• Параллелограмм
• Антипризма
• Параллелепипед

Ссылки