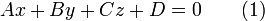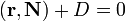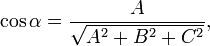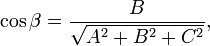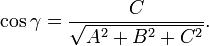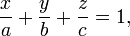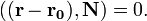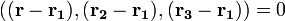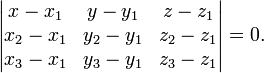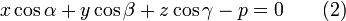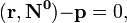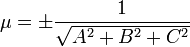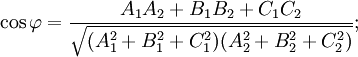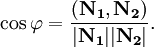- Плоскость (математика)
-
Плоскость (математика)
Пло́скость — одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Уравнение плоскости впервые встречается у А. К. Клеро (1731), уравнение плоскости в отрезках, по-видимому, впервые встречается у Г.Ламе (1816—1818), нормальное уравнение ввёл Л. О. Гессе (1861).
Содержание
Некоторые характеристические свойства плоскости
- Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки;
- Плоскость — множество точек, равноотстоящих от двух заданных точек.
Аналогично отрезку и интервалу, плоскость не включающую крайние точки можно назвать интервальной плоскостью или открытой плоскостью.
Уравнения плоскоcти
Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.
- Общее уравнение (полное) плоскости
где A,B,C и D — постоянные, причём A,B и C одновременно не равны нулю; в векторной форме:
где
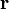 — радиус-вектор точки M(x,y,z), вектор
— радиус-вектор точки M(x,y,z), вектор 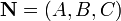 перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора
перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора 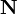 :
:Если один из коэффициентов в уравнении П. равен нулю, уравнение называется неполным. При D = 0 П. проходит через начало координат, при A = 0 (или B = 0, C = 0) П. параллельна оси Ox (соответствённо Oy или Oz). При A = B = 0 (A = C = 0, или B = C = 0) П. параллельна плоскости Oxy (соответственно Oxz или Oyz).
- Уравнение плоскости в отрезках:
где a = − D / A, b = − D / B, c = − D / C — отрезки, отсекаемые П. на осях Ox,Oy и Oz.
- Уравнение плоскости, проходящей через точку M(x0,y0,z0) перпендикулярно вектору нормали
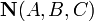 :
:
- A(x − x0) + B(y − y0) + C(z − z0) = 0;
в векторной форме:
- Уравнение плоскости, проходящей через три заданные точки M(xi,yi,zi), не лежащие на одной прямой:
(смешанное произведение векторов), иначе
- Нормальное (нормированное) уравнение плоскости
в векторной форме:
где
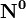 - единичный вектор, p — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель
- единичный вектор, p — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель(знаки μ и D противоположны).
Расстояние от точки до плоскости
Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.
- Отклонение точки M1(x1,y1,z1) от плоскости заданной нормированным уравнением (2)
δ = x1cosα + y1cosβ + z1cosγ − p; -
- δ > 0,если Mi и начало координат лежат по разные стoроны плоскости, в противоположном случае δ < 0. Расстояние от точки до плоскости равно | δ | .
- Расстояние ρ от точки M0(x0,y0,z0), до плоскости, заданной уравнением ax + by + cz + d = 0, вычисляется по формуле:
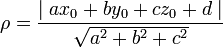
Расстояние между параллельными плоскостями
- Расстояние между плоскостями, заданными уравнениями Ax + By + Cz + D1 и Ax + By + Cz + D2:
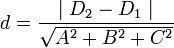
- Расстояние между плоскостями, заданными уравнениями
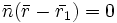 и
и 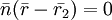 :
:
![d=\frac{\mid[\bar r_2 - \bar r_1, \bar n]\mid}{\mid\bar n\mid}](/pictures/wiki/files/55/7d9f7f3891bc3dfb0b04dd8cb331d71c.png)
Связанные понятия
- Угол между двумя плоскостями. Если уравнения П. заданы в виде (1), то
Если в векторной форме, то
- Плоскости параллельны, если
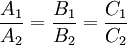 или
или ![[\mathbf{N_1}, \mathbf{N_2}]=0.](/pictures/wiki/files/48/098d72c21d8bb4a70984cbe225a4ebd1.png)
- Плоскости перпендикулярны, если
- A1A2 + B1B2 + C1C2 = 0 или
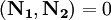 .
.
- Пучок плоскостей — уравнение любой П., проходящей через линию пересечения двух плокостей
- α(A1x + B1y + C1z) + β(A2x + B2y + C2z) = 0,
где α и β — любые числа, не равные одновременно нулю.
Плоскости в четырёхмерном пространстве
Если в четырёхмерном пространстве две плоскости лежат в одной гиперплоскости, то они могут либо быть параллельными (в частности, совпадать), либо пересекаться по линии.
Если же две плоскости не лежат в одной гиперплоскости, то они либо не пересекаются (скрещиваются, подобно тому как в трёхмерном пространстве скрещиваются прямые), либо имеют ровно одну общую точку.
Пересечение двух плоскостей в точке (а не по линии, как в трёхмерном пространстве) можно проиллюстрировать следующим примером. Пусть дана система декартовых координат x y z t. Пусть две плоскости α и β проходят через начало координат, причём плоскость α содержит координатные прямые x и y, а плоскость β содержит координатные прямые z и t. Соответственно у всех точек плоскости α координаты z и t равны 0, а у всех точек плоскости β координаты x и y равны 0. Тогда очевидно, что единственная точка, которая может принадлежать обеим плоскостям — это точка (0,0,0,0).
Литература
Ильин В. А., Позняк Э. Г. Аналитическая геометрия. — М.: ФИЗМАТЛИТ, 2002. — 240 с.
Wikimedia Foundation. 2010.