- Тессеракт
-
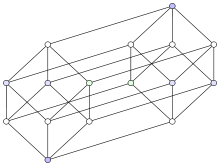
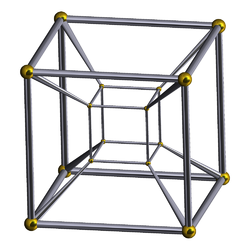 Диаграмма Шлегеля для тессеракта. Изображена проекция (перспектива) четырёхмерного куба на трёхмерное пространство
Диаграмма Шлегеля для тессеракта. Изображена проекция (перспектива) четырёхмерного куба на трёхмерное пространство
Тессеракт (от др.-греч. τέσσερες ἀκτῖνες — четыре луча) — четырёхмерный гиперкуб — аналог куба в четырёхмерном пространстве.
Согласно Оксфордскому словарю, слово tesseract было придумано и начало использоваться в 1888 Чарльзом Говардом Хинтоном (1853—1907) в его книге «Новая эра мысли». Позже некоторые люди назвали ту же самую фигуру тетракубом (греч. τετρα — четыре) — четырёхмерным кубом.
Содержание
Геометрия
Обычный тессеракт в евклидовом четырёхмерном пространстве определяется как выпуклая оболочка точек (±1, ±1, ±1, ±1). Иначе говоря, он может быть представлен в виде следующего множества:
Тессеракт ограничен восемью гиперплоскостями
 , пересечение которых с самим тессерактом задаёт его трёхмерные грани (являющиеся обычными кубами). Каждая пара непараллельных трёхмерных граней пересекается, образуя двумерные грани (квадраты), и так далее. Окончательно, тессеракт обладает 8 трёхмерными гранями, 24 двумерными, 32 рёбрами и 16 вершинами.
, пересечение которых с самим тессерактом задаёт его трёхмерные грани (являющиеся обычными кубами). Каждая пара непараллельных трёхмерных граней пересекается, образуя двумерные грани (квадраты), и так далее. Окончательно, тессеракт обладает 8 трёхмерными гранями, 24 двумерными, 32 рёбрами и 16 вершинами.Популярное описание
Попытаемся представить себе, как будет выглядеть гиперкуб, не выходя из трёхмерного пространства.
В одномерном «пространстве» — на линии — выделим отрезок АВ длиной L. На двумерной плоскости на расстоянии L от АВ нарисуем параллельный ему отрезок DC и соединим их концы. Получится квадрат CDBA. Повторив эту операцию с плоскостью, получим трёхмерный куб CDBAGHFE. А сдвинув куб в четвёртом измерении (перпендикулярно первым трём) на расстояние L, мы получим гиперкуб CDBAGHFEKLJIOPNM.
Построение тессеракта на плоскостиОдномерный отрезок АВ служит стороной двумерного квадрата CDBA, квадрат — стороной куба CDBAGHFE, который, в свою очередь, будет стороной четырёхмерного гиперкуба. Отрезок прямой имеет две граничные точки, квадрат — четыре вершины, куб — восемь. В четырёхмерном гиперкубе, таким образом, окажется 16 вершин: 8 вершин исходного куба и 8 сдвинутого в четвёртом измерении. Он имеет 32 ребра — по 12 дают начальное и конечное положения исходного куба, и ещё 8 рёбер «нарисуют» восемь его вершин, переместившихся в четвёртое измерение. Те же рассуждения можно проделать и для граней гиперкуба. В двумерном пространстве она одна (сам квадрат), у куба их 6 (по две грани от переместившегося квадрата и ещё четыре опишут его стороны). Четырёхмерный гиперкуб имеет 24 квадратные грани — 12 квадратов исходного куба в двух положениях и 12 квадратов от двенадцати его рёбер.
Как сторонами квадрата являются 4 одномерных отрезка, а сторонами (гранями) куба являются 6 двухмерных квадратов, так и для «четырёхмерного куба» (тессеракта) сторонами являются 8 трёхмерных кубов. Пространства противоположных пар кубов тессеракта (то есть трёхмерные пространства, которым эти кубы принадлежат) параллельны. На рисунке это кубы: CDBAGHFE и KLJIOPNM, CDBAKLJI и GHFEOPNM, EFBAMNJI и GHDCOPLK, CKIAGOME и DLJBHPNF.
Аналогичным образом можно продолжить рассуждения для гиперкубов большего числа измерений, но гораздо интереснее посмотреть, как для нас, жителей трёхмерного пространства, будет выглядеть четырёхмерный гиперкуб. Воспользуемся для этого уже знакомым методом аналогий.
Возьмём проволочный куб ABCDHEFG и поглядим на него одним глазом со стороны грани. Мы увидим и можем нарисовать на плоскости два квадрата (ближнюю и дальнюю его грани), соединённые четырьмя линиями — боковыми рёбрами. Аналогичным образом четырёхмерный гиперкуб в пространстве трёх измерений будет выглядеть как два кубических «ящика», вставленных друг в друга и соединённых восемью рёбрами. При этом сами «ящики» — трёхмерные грани — будут проецироваться на «наше» пространство, а линии, их соединяющие, протянутся в направлении четвёртой оси. Можно попытаться также представить себе куб не в проекции, а в пространственном изображении.
Подобно тому, как трёхмерный куб образуется квадратом, сдвинутым на длину грани, куб, сдвинутый в четвёртое измерение, сформирует гиперкуб. Его ограничивают восемь кубов, которые в перспективе будут выглядеть как некая довольно сложная фигура. Сам же четырёхмерный гиперкуб состоит из бесконечного количества кубов, подобно тому как трёхмерный куб можно «нарезать» на бесконечное количество плоских квадратов.
Разрезав шесть граней трёхмерного куба, можно разложить его в плоскую фигуру — развёртку. Она будет иметь по квадрату с каждой стороны исходной грани плюс ещё один — грань, ей противоположную. А трёхмерная развёртка четырёхмерного гиперкуба будет состоять из исходного куба, шести кубов, «вырастающих» из него, плюс ещё одного — конечной «гиперграни».
Свойства тессеракта представляют собой продолжение свойств геометрических фигур меньшей размерности в четырёхмерное пространство.
Проекции
На двумерное пространство
Данная структура сложна для воображения, но возможно спроектировать тессеракт в двумерные или трёхмерные пространства. Кроме того, проектирование на плоскость позволяет легко понять расположение вершин гиперкуба. Таким образом, можно получить изображения, которые больше не отражают пространственные отношения в пределах тессеракта, но которые иллюстрируют структуру связи вершин, как в следующих примерах:
 Третья картинка демонстрирует тессеракт в изометрии, относительно точки построения. Это представление представляет интерес при использовании тессеракта как основания для топологической сети, чтобы связать многократные процессоры в параллельных вычислениях.
Третья картинка демонстрирует тессеракт в изометрии, относительно точки построения. Это представление представляет интерес при использовании тессеракта как основания для топологической сети, чтобы связать многократные процессоры в параллельных вычислениях.
На трёхмерное пространство
Одна из проекций тессеракта на трёхмерное пространство представляет собой два вложенных трёхмерных куба, соответствующие вершины которых соединены между собой отрезками. Внутренний и внешний кубы имеют разные размеры в трёхмерном пространстве, но в четырёхмерном пространстве это равные кубы. Для понимания равности всех кубов тессеракта была создана вращающаяся модель тессеракта.
- Шесть усечённых пирамид по краям тессеракта — это изображения равных шести кубов. Однако эти кубы для тессеракта — как квадраты (грани) для куба. Но на самом деле тессеракт можно разделить на бесконечное количество кубов, как куб — на бесконечное количество квадратов, или квадрат — на бесконечное число отрезков.
Ещё одна интересная проекция тессеракта на трёхмерное пространство представляет собой ромбододекаэдр с проведёнными четырьмя его диагоналями, соединяющими пары противоположных вершин при больших углах ромбов. При этом 14 из 16 вершин тессеракта проецируются в 14 вершин ромбододекаэдра, а проекции 2 оставшихся совпадают в его центре. В такой проекции на трёхмерное пространство сохраняются равенство и параллельность всех одномерных, двухмерных и трёхмерных сторон.
Стереопара
Стереопара тессеракта изображается как две проекции на трёхмерное пространство. Такое изображение тессеракта разрабатывалось с целью представить глубину, как четвёртое измерение. Стереопара рассматривается так, чтобы каждый глаз видел только одно из этих изображений, возникает стереоскопическая картина, воспроизводящая глубину тессеракта.
Развёртка тессеракта
Поверхность тессеракта может быть развёрнута в восемь кубов (аналогично тому, как поверхность куба может быть развёрнута в шесть квадратов). Существует 261 различная развёртка тессеракта[1]. Развёртки тессеракта могут быть подсчитаны нанесением на граф соединённых углов.
Тессеракт в искусстве
- У Эдвине А. «Новая Равнина Абботта», гиперкуб выступает рассказчиком.
- В одном эпизоде «Приключений Джимми Нейтрона» «мальчик-гений» Джимми изобретает четырёхмерный гиперкуб, идентичный фолдбоксу из романа «Дорога славы» (1963) Роберта Хайнлайна.
- Роберт Э. Хайнлайн упоминал гиперкубы, по крайней мере, в трёх научно-фантастических рассказах. В «Доме четырёх измерений» («Дом, который построил Тил», 1940) он описал дом, построенный как развёртка тессеракта, а затем вследствие землетрясения «сложившийся» в четвёртом измерении и ставший «реальным» тессерактом.
- В романе «Дорога славы» Хайнлайна описана гиперразмерная шкатулка, которая была изнутри больше, чем снаружи.
- Рассказ Генри Каттнера «Все тенали бороговы» описывает развивающую игрушку для детей из далёкого будущего, по строению похожую на тессеракт.
- В романе Алекса Гарленда (1999), термин «тессеракт» используется для трёхмерной развёртки четырёхмерного гиперкуба, а не гиперкуба непосредственно. Это метафора, призванная показать, что познающая система должна быть шире познаваемой.
- Сюжет фильма «Куб 2: Гиперкуб» сосредотачивается на восьми незнакомцах, пойманных в ловушку в «гиперкубе», или сети связанных кубов.
- Телесериал «Андромеда» использует тессеракт-генераторы как устройство заговора. Они прежде всего предназначены, чтобы управлять пространством и временем.
- Картина «Распятие на кресте» (Corpus Hypercubus) Сальвадора Дали (1954).
- Комиксы «Nextwave comic book» изображают средство передвижения, включающее в себя 5 зон тессеракта.
- В альбоме Voivod Nothingface одна из композиций названа «В моём гиперкубе».
- В романе Энтони Пирса «Маршрут Куба» одна из орбитальных лун Международной ассоциации развития называется тессерактом, который был сжат в 3 измерения.
- В сериале «Школа „Чёрная дыра“» в третьем сезоне есть серия «Тессеракт». Лукас нажимает на секретную кнопку и школа начинает «складываться как математический тессеракт».
- Термин «тессеракт» и производный от него термин «тессировать» встречается в повести Мадлен Л’Энгл «Складка времени».
- TesseracT название британской джент группы.
- В серии фильмов Кинематографическая вселенная Marvel Тессеракт — это ключевой элемент сюжета, космический артефакт в форме гиперкуба.
- В рассказе Роберта Шекли «Мисс Мышка и четвертое измерение» один писатель-эзотерик, знакомец автора, пытается увидеть тессеракт, часами глядя на сконструированный им прибор: шар на ножке с воткнутыми в него стержнями, на которые насажены кубы, обклеенные всеми подряд эзотерическими символами. В рассказе упоминается труд Хинтона.
- В фильмах Первый Мститель, Мстители. Тессеракт-энергия все вселенной
Другие названия
- Гексадекахорон (англ. Hexadecachoron)
- Октохорон (англ. Octachoron)
- Тетракуб
- 4-Куб
- Гиперкуб (если не оговаривается число измерений)
Примечания
Литература
- Charles H. Hinton. Fourth Dimension, 1904. ISBN 0-405-07953-2
- Martin Gardner, Mathmatical Carnival, 1977. ISBN 0-394-72349-X
- Ian Stewart, Concepts of Modern Mathematics, 1995. ISBN 0-486-28424-7
Ссылки
- На русском языке
- получение из развертки
- Вращающийся стереоскопический гиперкуб
- Гиперкуб
- Программа Transformator4D. Формирование моделей трёхмерных проекций четырёхмерных объектов (в том числе и Гиперкуба).
- Программа, реализующая построение тессеракта и все его афинные преобразования, с исходниками на С++.
- Стереопара тессеракта с ребрами одинаковой длины.
- На английском языке
- Tesseract
- Cut The Knot! The Tesseract
- Charles Howard Hinton
- A four dimensional version of Rubik’s Cube
- Fourth Dimension: Tetraspace
- Mushware Limited — программа вывода тессеракта (Tesseract Trainer, лицензия совместима с GPLv2) и шутер от первого лица в четырёхмерном пространстве (Adanaxis; графика, в основном, трёхмерная; есть версия под GPL в репозиториях ОС).
Многогранники Правильные
(Платоновы тела)Трёхмерные Правильный тетраэдр • Куб • Октаэдр • Додекаэдр • Икосаэдр Четырёхмерные 6 правильных многогранников Большей размерности N-мерный куб • N-мерный октаэдр • N-мерный тетраэдр Звёздчатый додекаэдр • Звёздчатый икосододекаэдр • Звёздчатый икосаэдр • Звёздчатый многогранник • Звёздчатый октаэдр Выпуклые Архимедовы тела Кубооктаэдр • Икосододекаэдр • Усечённый тетраэдр • Усечённый октаэдр • Усечённый икосаэдр • Усечённый куб • Усечённый додекаэдр • Ромбокубоктаэдр • Ромбоикосододекаэдр • Ромбоусечённый кубоктаэдр • Ромбоусечённый икосододекаэдр • Курносый куб • Курносый додекаэдр • Усечённый кубооктаэдр • Усечённый икосододекаэдр • Правильная призма • Антипризма Каталановы тела Ромбододекаэдр • Ромботриаконтаэдр • Триакистетраэдр • Тетракисгексаэдр • Пентакисдодекаэдр • Триакисоктаэдр • Триакисикосаэдр • Дельтоидальный икоситетраэдр • Дельтоидальный гексеконтаэдр •Пентагональный икоситетраэдр • Пентагональный гексеконтаэдр • Дисдакисдодекаэдр • Дисдакистриаконтаэдр Без полной пространственной симметрии Пирамида • Призма • Бипирамида • Антипризма • Зоноэдр • Параллелепипед • Ромбоэдр •Призматоид• Усечённая пирамида• Пентагондодекаэдр • Параллелоэдр Формулы,
теоремы,
теорииПрочее Ортоцентрический тетраэдр • Равногранный тетраэдр • Прямоугольный параллелепипед • Группа многогранника • Двенадцатигранники • Телесный угол • Единичный куб • Изгибаемый многогранник • Развёртка • Символ Шлефли • Многомерные (N-мерный тетраэдр • Тессеракт • Пентеракт • Хексеракт • Хептеракт • Октеракт • Энтенеракт • Декеракт • Гиперкуб)
Категории:- Многогранники
- Геометрические фигуры
- Правильные многогранники
- Многомерная евклидова геометрия
Wikimedia Foundation. 2010.


![[-1, 1]^4 \equiv \{(x_1,x_2,x_3,x_4) \,:\, -1 \leq x_i \leq 1 \}.](b3aa12c5db4d339d52911c8f7df414e5.png)