Гиперкуб

У этого термина существуют и другие значения, см. Куб 2: Гиперкуб.

Гиперкуб — обобщение куба на случай с произвольным числом измерений.

Гиперкубом размерности Ν называется множество точек в Ν-мерном евклидовом пространстве, удовлетворяющее неравенствам $\forall i: -\frac{a}{2}<x_i<\frac{a}{2}$, где a — длина ребра гиперкуба.

Также можно определить гиперкуб как декартово произведение Ν равных отрезков.

Также можно сказать, что Ν-куб — это фигура, каждая вершина которой связана рёбрами с Ν другими вершинами; Ν, в свою очередь, определяет размерность этой фигуры. Или же, Ν-мерный куб образуется Ν парами параллельных (Ν-1)-плоскостей, то есть имеет 2Ν гиперграни, каждая из которых является (Ν-1)-кубом.

Свойства гиперкуба

Свойство	Значение
Длина ребра	a
Размерность	N
Гиперобъём	$V_N = a^N$
Гиперплощадь поверхности	$S_N = {2 N a}^{N-1}$

В информатике

Гиперкуб — сетевая топология, в которой узлы являются вершинами графа многомерного куба.

Различные гиперкубы

N-Куб	Изображение (двумерная проекция)	Название	Точек (0)	Отрезков (1)	Квадратов (2)	Кубов (3)	Тессерактов (4)	Пентерактов (5)	Хексерактов (6)	Хептерактов (7)	Октерактов (8)	Энтенерактов (9)	Декерактов (10)
0-куб		Точка	1
1-куб		Отрезок	2	1
2-куб		Квадрат	4	4	1
3-куб		Куб	8	12	6	1
4-куб		Тессеракт	16	32	24	8	1
5-куб	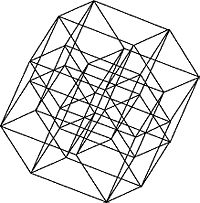	Пентеракт	32	80	80	40	10	1
6-куб	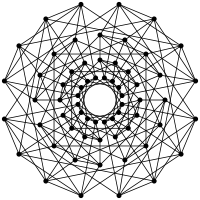	Хексеракт	64	192	240	160	60	12	1
7-куб	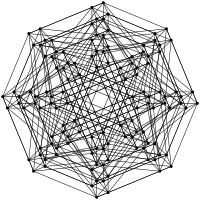	Хептеракт	128	448	672	560	280	84	14	1
8-куб	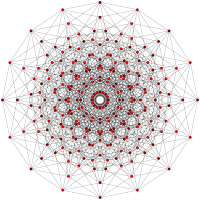	Октеракт	256	1024	1792	1792	1120	448	112	16	1
9-куб	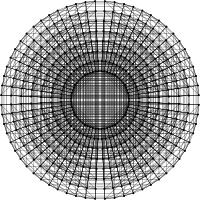	Энтенеракт[источник не указан 373 дня]	512	2304	4608	5376	4032	2016	672	144	18	1
10-куб		Декеракт[источник не указан 373 дня]	1024	5120	11520	15360	13440	8064	3360	960	180	20	1

Гиперкуб в художественной литературе

• Роберт Хайнлайн. Дом, который построил Тил.
• Роберт Шекли. Мисс Мышка и четвертое измерение.
• Эдвин Эбботт. Флатландия

См. также

• Правильные N-мерные многогранники

Ссылки

• Анимация развертки из квадрата до октеракта (и стереопара)