Полуправильный многогранник

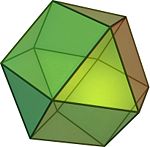
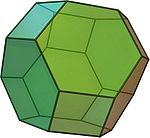
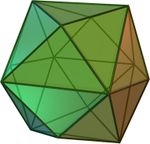
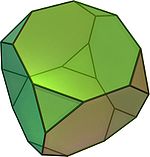
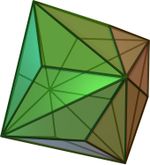
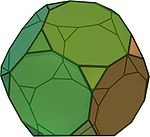
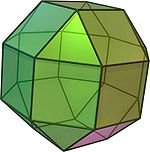
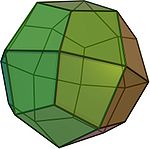
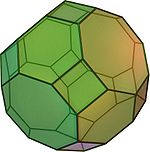
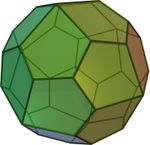
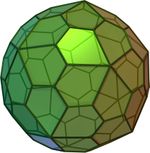
Полуправильные многогранники — в общем случае это различные выпуклые многогранники, имеющие определённые признаки правильных, такие как одинаковость всех граней или являемость всех граней правильными многоугольниками, а также пространственная симметрия. Определение может варьироваться и включать различные типы многогранников, но в первую очередь сюда относятся архимедовы тела.

Архимедовы тела

Архимедовы тела — выпуклые многогранники, обладающие двумя свойствами:

• Все грани являются правильными многоугольниками двух или более типов (если все грани — правильные многоугольники одного типа, это — правильный многогранник);
• Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую. В частности,
  • Все многогранные углы при вершинах конгруэнтны.

Первое построение полуправильных многогранников приписывается Архимеду, хотя соответствующие работы утеряны.

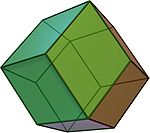
Каталановы тела

Двойственные архимедовым телам, так называемые Каталановы тела, имеют конгруэнтные грани, равные двугранные углы и правильные многогранные углы. Каталановы тела тоже иногда называют полуправильными многогранниками. В этом случае полуправильными многогранниками считается совокупность архимедовых и каталановых тел. Архимедовы тела являются полуправильными многогранниками в том смысле, что их грани — правильные многоугольники, но они не одинаковы, а каталановы — в том смысле, что их грани одинаковы, но не являются правильными многоугольниками; при этом для тех и других сохраняется условие одного из типов пространственной симметрии: тетраэдрического, октаэдрического или икосаэдрического.

То есть, полуправильными в этом случае называются тела, у которых отсутствует только одно из первых двух из следующих свойств правильных тел:

• Все грани являются правильными многоугольниками;
• Все грани одинаковы;
• Тело относится к одному из трёх существующих типов пространственной симметрии.

Архимедовы — тела, у которых отсутствует второе свойство, у каталановых отсутствует первое, третье свойство сохраняется для обоих видов тел.

Существует 13 архимедовых тел, два из которых (курносый куб и курносый додекаэдр) не являются зеркально-симметричными и имеют левую и правую формы. Соответственно, существует 13 каталановых тел.

Многогранник — архимедово тело	Грани	Вершины	Рёбра	Конфигурация вершины	Двойственный — каталаново тело	Группа симметрии
Кубооктаэдр	8 треугольников 6 квадратов	12	24	3,4,3,4	Ромбододекаэдр	Oh
Икосододекаэдр	20 треугольников 12 пятиугольников	30	60	3,5,3,5	Ромботриаконтаэдр	Ih
Усечённый тетраэдр	4 треугольника 4 шестиугольника	12	18	3,6,6	Триакистетраэдр	Th
Усечённый октаэдр	6 квадратов 8 шестиугольников	24	36	4,6,6	Преломлённый куб (Тетракисгексаэдр)	Oh
Усечённый икосаэдр	12 пятиугольников 20 шестиугольников	60	90	5,6,6	Пентакисдодекаэдр	Ih
Усечённый куб	8 треугольников 6 восьмиугольников	24	36	3,8,8	Триакисоктаэдр	Oh
Усечённый додекаэдр	20 треугольников 12 десятиугольников	60	90	3,10,10	Триакисикосаэдр	Ih
Ромбокубооктаэдр	8 треугольников 18 квадратов (6 — в кубическом положении, 12 — в ромбическом)	24	48	3,4,4,4	Дельтоидальный икоситетраэдр	Oh
Ромбоикосододекаэдр	20 треугольников 30 квадратов 12 пятиугольников	60	120	3,4,5,4	Дельтоидальный гексеконтаэдр	Ih
Ромбоусечённый кубооктаэдр	12 квадратов 8 шестигольников 6 восьмиугольников	48	72	4,6,8	Гекзакисоктаэдр	Oh
Ромбоусечённый икосододекаэдр	30 квадратов 20 шестиугольников 12 десятиугольников	120	180	4,6,10	Гекзакисикосаэдр	Ih
Курносый куб	32 треугольника 6 квадратов	24	60	3,3,3,3,4	Пентагональный икоситетраэдр	O
Курносый додекаэдр	80 треугольников 12 пятиугольников	60	150	3,3,3,3,5	Пентагональный гексеконтаэдр	I

Примеры

Существует две бесконечные последовательности полуправильных многогранников — правильные призмы и антипризмы.

См. также

• Правильный многогранник
• Каталановы тела
• Звёздчатый многогранник
• Призма
• Антипризма

Ссылки

• В. Г. Ашкинузе О числе полуправильных многогранников // Математическое просвещение. Вторая серия. — 1957. — В. 1. — С. 107-118.