- Комплексное число
-
Запрос «Мнимая величина» перенаправляется сюда; см. также другие значения.Запрос «Re» перенаправляется сюда; см. также другие значения.Запрос «Im» перенаправляется сюда; см. также другие значения.
Ко́мпле́ксные[1] чи́сла (устар. Мнимые числа[2]), — расширение поля вещественных чисел, обычно обозначается
 . Любое комплексное число может быть представлено как формальная сумма
. Любое комплексное число может быть представлено как формальная сумма  , где
, где  и
и  — вещественные числа,
— вещественные числа,  — мнимая единица[3].
— мнимая единица[3].Комплексные числа образуют алгебраически замкнутое поле — это означает, что многочлен степени
 с комплексными коэффициентами имеет ровно
с комплексными коэффициентами имеет ровно  комплексных корней (основная теорема алгебры). Это одна из главных причин широкого применения комплексных чисел в математических исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать многие математические модели, применяемые в математической физике и в естественных науках — электротехнике, гидродинамике, картографии, квантовой механике, теории колебаний и многих других.
комплексных корней (основная теорема алгебры). Это одна из главных причин широкого применения комплексных чисел в математических исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать многие математические модели, применяемые в математической физике и в естественных науках — электротехнике, гидродинамике, картографии, квантовой механике, теории колебаний и многих других.Содержание
Определения
Поле комплексных чисел можно понимать как расширение поля вещественных чисел, в котором многочлен
 имеет корень. Следующие две элементарные модели показывают, что непротиворечивое построение такой системы чисел возможно. Оба приведенных определения приводят к изоморфным расширениям поля вещественных чисел
имеет корень. Следующие две элементарные модели показывают, что непротиворечивое построение такой системы чисел возможно. Оба приведенных определения приводят к изоморфным расширениям поля вещественных чисел  , как и любые другие конструкции поля разложения многочлена
, как и любые другие конструкции поля разложения многочлена  .
.Стандартная модель
Комплексное число
 можно определить как упорядоченную пару вещественных чисел
можно определить как упорядоченную пару вещественных чисел  . Введём операции сложения и умножения таких пар следующим образом:
. Введём операции сложения и умножения таких пар следующим образом:Вещественные числа являются в этой модели подмножеством множества комплексных чисел и представлены парами вида
 , причём операции с такими парами согласованы с обычными сложением и умножением вещественных чисел. Ноль представляется парой
, причём операции с такими парами согласованы с обычными сложением и умножением вещественных чисел. Ноль представляется парой  единица —
единица —  а мнимая единица —
а мнимая единица —  На множестве комплексных чисел ноль и единица обладают теми же свойствами, что и на множестве вещественных, а квадрат мнимой единицы, как легко проверить, равен
На множестве комплексных чисел ноль и единица обладают теми же свойствами, что и на множестве вещественных, а квадрат мнимой единицы, как легко проверить, равен  , то есть
, то есть 
Несложно показать, что определённые выше операции имеют те же свойства, что и аналогичные операции с вещественными числами. Исключением являются только свойства, связанные с отношением порядка (больше-меньше), потому что расширить порядок вещественных чисел, включив в него все комплексные числа так, чтобы операции по-прежнему были согласованы с порядком, невозможно.
Матричная модель
Комплексные числа можно также определить как семейство вещественных матриц вида
с обычным матричным сложением и умножением. Действительной единице будет соответствовать
мнимой единице —
Замечания
Ошибочно определение числа
 как единственного числа, удовлетворяющего уравнению
как единственного числа, удовлетворяющего уравнению  , так как число
, так как число  также удовлетворяет этому уравнению.
также удовлетворяет этому уравнению.Следует также заметить, что выражение
 , ранее часто использовавшееся вместо
, ранее часто использовавшееся вместо  , не вполне корректно, так как алгебраический корень определяется над множеством неотрицательных чисел. Вплоть до конца XIX века запись вроде
, не вполне корректно, так как алгебраический корень определяется над множеством неотрицательных чисел. Вплоть до конца XIX века запись вроде  считалась допустимой, но в настоящее время, во избежание ошибок, принято записывать это выражение как
считалась допустимой, но в настоящее время, во избежание ошибок, принято записывать это выражение как  . Пример возможной ошибки при неосторожном использовании устаревшей записи:
. Пример возможной ошибки при неосторожном использовании устаревшей записи:в то время как правильная запись приводит к иному ответу:
Действия над комплексными числами
- Сравнение
 означает, что
означает, что  и
и  (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
(два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
- Сложение
- Вычитание
- Умножение
- Деление
Геометрическая модель
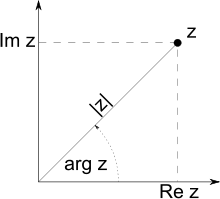
Рассмотрим плоскость с прямоугольной системой координат. Каждому комплексному числу
 сопоставим точку плоскости с координатами
сопоставим точку плоскости с координатами  (а также радиус-вектор, соединяющий начало координат с этой точкой). Такая плоскость называется комплексной. Вещественные числа на ней занимают горизонтальную ось, мнимая единица изображается единицей на вертикальной оси; по этой причине горизонтальная и вертикальная оси называются соответственно вещественной и мнимой осями.
(а также радиус-вектор, соединяющий начало координат с этой точкой). Такая плоскость называется комплексной. Вещественные числа на ней занимают горизонтальную ось, мнимая единица изображается единицей на вертикальной оси; по этой причине горизонтальная и вертикальная оси называются соответственно вещественной и мнимой осями.Часто бывает удобно рассматривать на комплексной плоскости также полярную систему координат, в которой координатами точки являются расстояние до начала координат (модуль) и угол радиус-вектора точки (показанного синей стрелкой на рисунке) с горизонтальной осью (аргумент). Подробнее см. ниже.
В этом наглядном представлении сумма комплексных чисел соответствует векторной сумме соответствующих радиус-векторов. При перемножении комплексных чисел их модули перемножаются, а аргументы складываются. Если модуль второго сомножителя равен 1, то умножение на него геометрически означает поворот радиус-вектора первого числа на угол, равный аргументу второго числа. Этот факт объясняет широкое использование комплексного представления в теории колебаний, где вместо терминов «модуль» и «аргумент» используются термины «амплитуда» и «фаза».
Геометрическая модель комплексных чисел широко используется в планиметрии: многие планиметрические теоремы можно доказать как некоторые комплексные тождества. Часто этот метод даёт наиболее простое доказательство.
Связанные определения
Пусть
 — комплексное число, где
— комплексное число, где  и
и  — вещественные числа. Числа
— вещественные числа. Числа  или
или  и
и  или
или  называются соответственно вещественной и мнимой (аналогично англ. real, imaginary) частями
называются соответственно вещественной и мнимой (аналогично англ. real, imaginary) частями  .
.- Если
 , то
, то  называется мнимым или чисто мнимым числом.
называется мнимым или чисто мнимым числом. - Если
 , то
, то  является действительным (вещественным) числом.
является действительным (вещественным) числом.
Модуль и аргумент
Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же, расстояние между точкой комплексной плоскости, соответствующей этому числу, и началом координат).
Модуль комплексного числа
 обозначается
обозначается  и определяется выражением
и определяется выражением  . Часто обозначается буквами
. Часто обозначается буквами  или
или  . Если
. Если  является вещественным числом, то
является вещественным числом, то  совпадает с абсолютной величиной этого вещественного числа.
совпадает с абсолютной величиной этого вещественного числа.Для любых
 имеют место следующие свойства модуля. :
имеют место следующие свойства модуля. :- 1)
 , причём
, причём  тогда и только тогда, когда
тогда и только тогда, когда  ;;
;; - 2)
 (неравенство треугольника);
(неравенство треугольника); - 3)
 ;
; - 4)
 .
.
Из третьего свойства следует
 , где
, где  . Данное свойство модуля вместе с первыми двумя свойствами вводят на множестве комплексных чисел структуру двумерного нормированного пространства над полем
. Данное свойство модуля вместе с первыми двумя свойствами вводят на множестве комплексных чисел структуру двумерного нормированного пространства над полем  .
.- 5) Для пары комплексных чисел
 и
и  модуль их разности
модуль их разности  равен расстоянию между соответствующими точками комплексной плоскости.
равен расстоянию между соответствующими точками комплексной плоскости.
Угол
 (в радианах) радиус-вектора точки, соответствующей числу
(в радианах) радиус-вектора точки, соответствующей числу  , называется аргументом числа
, называется аргументом числа  и обозначается
и обозначается  .
.- Из этого определения следует, что
 ;
;  ;
;  .
. - Для комплексного нуля значение аргумента не определено, для ненулевого числа
 аргумент определяется с точностью до
аргумент определяется с точностью до  , где
, где  — любое целое число.
— любое целое число. - Главным значением аргумента называется такое значение
 , что
, что  . Часто главное значение обозначается
. Часто главное значение обозначается  [4]. Главное значение аргумента обратного числа отличается знаком от аргумента исходного:
[4]. Главное значение аргумента обратного числа отличается знаком от аргумента исходного:  .
.
Сопряжённые числа
Если комплексное число
 , то число
, то число  называется сопряжённым (или комплексно сопряжённым) к
называется сопряжённым (или комплексно сопряжённым) к  (обозначается также
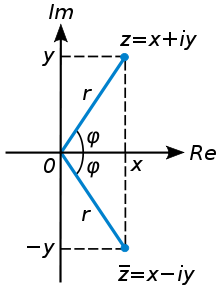
(обозначается также  ). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.
). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком.Переход к сопряжённому числу можно рассматривать как одноместную операцию; перечислим её свойства.
 (сопряжённое к сопряжённому есть исходное).
(сопряжённое к сопряжённому есть исходное).



Обобщение:
 , где
, где  — произвольный многочлен с вещественными коэффициентами.
— произвольный многочлен с вещественными коэффициентами.Значимость сопряжения объясняется тем, что оно является образующей группы Галуа
 .
.Представление комплексных чисел
Алгебраическая форма
Запись комплексного числа
 в виде
в виде  ,
,  , называется алгебраической формой комплексного числа.
, называется алгебраической формой комплексного числа.Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что
 ):
):Тригонометрическая и показательная формы
Если вещественную
 и мнимую
и мнимую  части комплексного числа выразить через модуль
части комплексного числа выразить через модуль  и аргумент
и аргумент  (
( ,
,  ), то всякое комплексное число
), то всякое комплексное число  , кроме нуля, можно записать в тригонометрической форме
, кроме нуля, можно записать в тригонометрической формеТакже может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:
где
 — расширение экспоненты для случая комплексного показателя степени.
— расширение экспоненты для случая комплексного показателя степени.Отсюда вытекают следующие широко используемые равенства:
Формула Муавра и извлечение корней из комплексных чисел
 Корни пятой степени из единицы (вершины пятиугольника)
Корни пятой степени из единицы (вершины пятиугольника)
Эта формула позволяет возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:
где
 — модуль, а
— модуль, а  — аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 году. Приведенная формуле справедлива при любом целом n, не обязательно положительном.
— аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 году. Приведенная формуле справедлива при любом целом n, не обязательно положительном.Аналогичная формула применима также и при вычислении корней
 -ой степени из ненулевого комплексного числа:
-ой степени из ненулевого комплексного числа:Отметим, что корни
 -й степени из ненулевого комплексного числа всегда существуют, и их количество равно
-й степени из ненулевого комплексного числа всегда существуют, и их количество равно  . На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного
. На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного  -угольника, вписанного в окружность радиуса
-угольника, вписанного в окружность радиуса ![\sqrt[n]{r}](0c1dda2d990c60ca5ef80cd446e594db.png) с центром в начале координат (см. рисунок).
с центром в начале координат (см. рисунок).История
Впервые, по-видимому, мнимые величины появились в известном труде «Великое искусство, или об алгебраических правилах» Кардано (1545), который счёл их непригодными к употреблению. Пользу мнимых величин, в частности, при решении кубического уравнения, в так называемом неприводимом случае (когда вещественные корни многочлена выражаются через кубические корни из мнимых величин), впервые оценил Бомбелли (1572). Он же дал некоторые простейшие правила действий с комплексными числами.
Выражения вида
 , появляющиеся при решении квадратных и кубических уравнений, стали называть «мнимыми» в XVI—XVII веках, однако даже для многих крупных ученых XVII века алгебраическая и геометрическая сущность мнимых величин представлялась неясной. Лейбниц, например, писал: «Дух божий нашёл тончайшую отдушину в этом чуде анализа, уроде из мира идей, двойственной сущности, находящейся между бытием и небытием, которую мы называем мнимым корнем из отрицательной единицы».[5]
, появляющиеся при решении квадратных и кубических уравнений, стали называть «мнимыми» в XVI—XVII веках, однако даже для многих крупных ученых XVII века алгебраическая и геометрическая сущность мнимых величин представлялась неясной. Лейбниц, например, писал: «Дух божий нашёл тончайшую отдушину в этом чуде анализа, уроде из мира идей, двойственной сущности, находящейся между бытием и небытием, которую мы называем мнимым корнем из отрицательной единицы».[5]Долгое время было неясно, все ли операции над комплексными числами приводят к комплексным результатам, или, например, извлечение корня может привести к открытию какого-то нового типа чисел. Задача о выражении корней степени
 из данного числа была решена в работах Муавра (1707) и Котса (1722).
из данного числа была решена в работах Муавра (1707) и Котса (1722).Символ
 предложил Эйлер (1777, опубл. 1794), взявший для этого первую букву слова лат. imaginarius. Он же распространил все стандартные функции, включая логарифм, на комплексную область. Эйлер также высказал в 1751 году мысль об алгебраической замкнутости поля комплексных чисел. К такому же выводу пришел д’Аламбер (1747), но первое строгое доказательство этого факта принадлежит Гауссу (1799). Гаусс и ввёл в широкое употребление термин «комплексное число» в 1831 году, хотя этот термин ранее использовал в том же смысле французский математик Лазар Карно в 1803 году.
предложил Эйлер (1777, опубл. 1794), взявший для этого первую букву слова лат. imaginarius. Он же распространил все стандартные функции, включая логарифм, на комплексную область. Эйлер также высказал в 1751 году мысль об алгебраической замкнутости поля комплексных чисел. К такому же выводу пришел д’Аламбер (1747), но первое строгое доказательство этого факта принадлежит Гауссу (1799). Гаусс и ввёл в широкое употребление термин «комплексное число» в 1831 году, хотя этот термин ранее использовал в том же смысле французский математик Лазар Карно в 1803 году.Геометрическое истолкование комплексных чисел и действий над ними появилось впервые в работе Весселя (1799). Первые шаги в этом направлении были сделаны Валлисом (Англия) в 1685 году. Современное геометрическое представление, иногда называемое «диаграммой Аргана», вошло в обиход после опубликования в 1806-м и 1814-м годах работы Ж. Р. Аргана, повторявшей независимо выводы Весселя. Термины «модуль», «аргумент» и «сопряжённое число» ввёл Коши.
Арифметическая модель комплексных чисел как пар вещественных чисел была построена Гамильтоном (1837); это доказало непротиворечивость их свойств. Гамильтон предложил и обобщение комплексных чисел — кватернионы, алгебра которых некоммутативна.
Вариации и обобщения
Функции комплексного переменного
- Гамма-функция
- Гиперболические функции
- Дзета-функция Римана
- Комплексный анализ
- Комплексный логарифм
- Показательная функция
- Степенная функция
- W-функция Ламберта
См. также
Примечания
- ↑ Двойное ударение указано согласно следующим источникам.
- Большая советская энциклопедия, 3-е изд. (1973), том 12, стр. 588, статья Ко́мпле́ксные числа.
- Советский энциклопедический словарь (1982), стр. 613, статья Ко́мпле́ксное число.
- Последнее издание «Словаря трудностей русского языка» (Розенталь Д. Э., Теленкова М. А., Айрис-пресс, 2005, стр. 273) указывает оба варианта: «ко́мплексные (компле́ксные) числа».
- В Большой российской энциклопедии (том 14, 2010 год) по необъяснённым причинам предлагаются одновременно ударения Компле́ксное число (стр. 691), но Ко́мплексный анализ (стр. 695).
- Орфографический словарь русского языка (6-е издание, 2010), Грамматический словарь русского языка (6-е издание, 2009), Русский орфографический словарь Российской академии наук под ред. В. В. Лопатина (2-е издание, 2004).
- ↑ «Математическая энциклопедия» / Главный редактор И. М. Виноградов. — М.: «Советская энциклопедия», 1979. — 1104 с. — (51[03] М34). — 148 800 экз.
- ↑ В теории электрических цепей, символ
 иногда заменяют на
иногда заменяют на  , чтобы не путать со стандартным обозначением электрического тока (
, чтобы не путать со стандартным обозначением электрического тока ( ).
). - ↑ Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1967. — С. 14-15.
- ↑ Клайн М. Математика. Утрата определённости. — М.: Мир, 1984. — С. 139.
Литература

Комплексные числа в Викиучебнике? 
Комплексные числа на Викискладе? - Арнольд В. И. Геометрия комплексных чисел, кватернионов и спинов, МЦНМО, 2002
- Елисеев В. И. «Введение в методы теории функций пространственного комплексного переменного», Центр научно-технического творчества молодежи Алгоритм. — М.:, НИАТ. — 1990. Шифр Д7-90/83308
- Понтрягин Л. Комплексные числа, Квант, № 3, 1982.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: ФИЗМАТЛИТ, 2001. — Т. II. — 680 с. — ISBN 5-9221-0156-0, 5-9221-0155-2, 5-9221-0436-5.
Ссылки
- Простой калькулятор комплексных чисел.
- CaRevol Jet — Формульный калькулятор комплексных чисел под Windows.

Натуральные числа 
Целые числа 
Рациональные числа 
Вещественные числа 
Комплексные числа 
Кватернионы Числовые системы Счётные
множестваНатуральные числа (  ) • Целые (
) • Целые ( ) • Рациональные (
) • Рациональные ( ) • Алгебраические (
) • Алгебраические ( ) • Периоды • Вычислимые • Арифметические
) • Периоды • Вычислимые • АрифметическиеВещественные числа
и их расширенияВещественные (  ) • Комплексные (
) • Комплексные ( ) • Кватернионы (
) • Кватернионы ( ) • Числа Кэли (октавы, октонионы) (
) • Числа Кэли (октавы, октонионы) ( ) • Седенионы (
) • Седенионы ( ) • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.)
) • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.)Другие
числовые системыКардинальные числа • Порядковые числа (трансфинитные, ординал) • p-адические • Супернатуральные числа См. также Двойные числа • Иррациональные числа • Трансцендентные • Числовой луч • Бикватернион Алгебра над кольцом Математика 2-мерная Элементы: Комплексные числа 4-мерная Элементы: Кватернионы 8-мерная Элементы: Числа Кэли (октонионы или октавы) 16-мерная Элементы: Седенионы См. также Гиперкомплексное число • Алгебра • Тело (алгебра) • Число • мнимая единица Теория множеств Категории:- Статьи с упоминанием устаревших значений
- Числа
- Комплексный анализ
Wikimedia Foundation. 2010.




















![z^n=[r(\cos\varphi+i\sin\varphi)]^n=r^n(\cos n\varphi+i\sin n\varphi),](2044ad877a6bc06a8013a667ecf5fb99.png)
![z^{1/n}=[r(\cos(\varphi+2\pi k)+i\sin(\varphi+2\pi k))]^{1/n}=](84d84f1b37cd60b746b3403e6bafa163.png)

