- Неравенство треугольника
-
Нера́венство треуго́льника в геометрии, функциональном анализе и смежных дисциплинах — это одно из интуитивных свойств расстояния. Оно утверждает, что длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон. Неравенство треугольника включается как аксиома в определение метрического пространства, нормы и т.д.; также, часто является теоремой в различных теориях.
Содержание
Евклидова геометрия
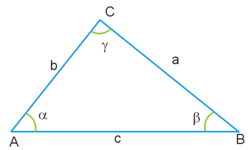
Пусть дан треугольник
 Тогда
Тогда  причём равенство
причём равенство  достигается только тогда, когда треугольник вырожден, и точка
достигается только тогда, когда треугольник вырожден, и точка  лежит строго между
лежит строго между  и
и  .
.Евклид в Началах доказывает неравенство треугольника следующим образом. Сначала доказывается теорема о том, что внешний угол треугольника больше внутреннего угла, с ним не смежного. Из неё выводится теорема о том, что против большей стороны треугольника лежит больший внутренний угол. Далее, методом от противного доказывается теорема о том, что против большего внутреннего угла треугольника лежит большая сторона. А из этой теоремы выводится неравенство треугольника.
Нормированное пространство
Пусть
 — нормированное векторное пространство, где
— нормированное векторное пространство, где  — произвольное множество, а
— произвольное множество, а  — определённая на
— определённая на  норма. Тогда по определению последней справедливо:
норма. Тогда по определению последней справедливо:Гильбертово пространство
В гильбертовом пространстве, неравенство треугольника является следствием неравенства Коши — Буняковского.
Метрическое пространство
Пусть
 — метрическое пространство, где
— метрическое пространство, где  — произвольное множество, а
— произвольное множество, а  — определённая на
— определённая на  метрика. Тогда по определению последней
метрика. Тогда по определению последнейВариации и обобщения
Обратное неравенство треугольника
Следствием неравенства треугольника в нормированном и метрическом пространствах являются следующие неравенства:
Неравенство треугольника для трёхгранного угла
См. также: Сферическая геометрияКаждый плоский угол выпуклого трёхгранного угла меньше суммы двух других его плоских углов.
Категории:- Метрическая геометрия
- Евклидова геометрия
- Линейная алгебра
- Неравенства
Wikimedia Foundation. 2010.