Гиперболические функции

Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями.

Определение

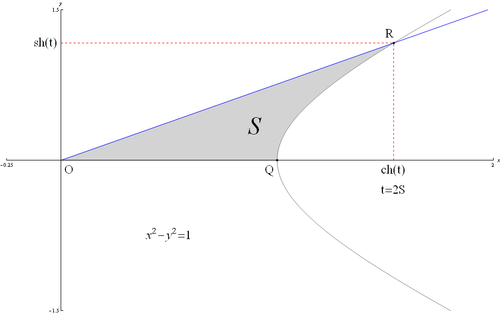Определение гиперболических функций через гиперболу

Гиперболические функции задаются следующими формулами:

• гиперболический синус:

$\operatorname{sh}x=\frac{e^x-e^{-x}}{2}$

(в англоязычной литературе обозначается $\sinh(x)$)

• гиперболический косинус:

$\operatorname{ch}x=\frac{e^x+e^{-x}}{2}$

(в англоязычной литературе обозначается $\cosh(x)$)

• гиперболический тангенс:

$\operatorname{th}x=\frac{\operatorname{sh}x}{\operatorname{ch}x} = \frac {e^x - e^{-x}} {e^x + e^{-x}} = \frac{e^{2x} - 1} {e^{2x} + 1}$

(в англоязычной литературе обозначается $\tanh(x)$)

• гиперболический котангенс:

$\operatorname{cth}x=\frac{1}{\operatorname{th}x}$

Иногда также определяются

• гиперболические секанс и косеканс:

$\operatorname{sech}x=\frac{1}{\operatorname{ch}x}$

$\operatorname{csch}x=\frac{1}{\operatorname{sh}x}$

Геометрическое определение

Параметризация гиперболического синуса (анимация).

Ввиду соотношения $\operatorname{ch}^2t-\operatorname{sh}^2t=1$ гиперболические функции дают параметрическое представление гиперболы $~x^2-y^2=1$ ($x=\operatorname{ch}t$, $y=\operatorname{sh}t$). При этом аргумент $t=2S$, где $S$ — площадь криволинейного треугольника $OQR$, взятая со знаком «+», если сектор лежит выше оси $OX$, и «−» в противоположном случае. Очевидно, что и гиперболические функции определяются через этот параметр, например, уравнения гиперболического синуса в параметрической форме: $x=t, y=f(t)$, где $f(t)$ — ордината точки гиперболы, соответствующей площади $t=2S$. Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом.

Свойства

Связь с тригонометрическими функциями

Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента.

$\operatorname{sh}x=-i\sin(ix),\quad \operatorname{ch}x=\cos(ix),\quad \operatorname{th}x=-i\operatorname{tg}(ix)$.

$\operatorname{sh}(ix) = i\operatorname{sin}x,\quad \operatorname{ch}(ix) = \cos x,\quad \operatorname{th}(ix)= i\operatorname{tg}x$.

Функция Гудермана связывает тригонометрические функции и гиперболические функции без привлечения комплексных чисел.

Важные соотношения

1. $\operatorname{ch}^2x-\operatorname{sh}^2x=1$ (Тождество)
2. Чётность:
   1. $\operatorname{sh}(-x)=-\operatorname{sh}x$
   2. $\operatorname{ch}(-x)=\operatorname{ch}x$
   3. $\operatorname{th}(-x)=-\operatorname{th}x$
3. Формулы сложения:
   1. $\operatorname{sh}(x \pm y)=\operatorname{sh}x\,\operatorname{ch}y \pm \operatorname{sh}y\,\operatorname{ch}x$
   2. $\operatorname{ch}(x \pm y)=\operatorname{ch}x\,\operatorname{ch}y \pm \operatorname{sh}y\,\operatorname{sh}x$
   3. $\operatorname{th}(x \pm y)=\frac{\operatorname{th}x \pm \operatorname{th}y}{1 \pm \operatorname{th}x\,\operatorname{th}y}$
   4. $\operatorname{cth}(x \pm y)=\frac{\operatorname{cth}x\,\operatorname{cth}y \pm 1}{\operatorname{cth}y \pm \operatorname{cth}x}$
4. Формулы двойного угла:
   1. $\operatorname{sh}2x=2\operatorname{ch}x\,\operatorname{sh}x=\frac{2\,\operatorname{th}x}{1-\operatorname{th}^2x}$
   2. $\operatorname{ch}2x=\operatorname{ch}^2x+\operatorname{sh}^2x=2\operatorname{ch}^2x-1=1+2\operatorname{sh}^2x=\frac{1+\operatorname{th}^2x}{1-\operatorname{th}^2x}$
   3. $\operatorname{th}2x=\frac{2\operatorname{th}x}{1+\operatorname{th}^2x}$
   4. $\operatorname{cth}2x=\frac{1}{2} (\operatorname{th}x+\operatorname{cth}x)$
   5. $\operatorname{th}x=\frac{\operatorname{ch}2x-1}{\operatorname{sh}2x}=\frac{\operatorname{sh}2x}{1+\operatorname{ch}2x}$
   6. $\operatorname{ch}2x \pm \operatorname{sh}2x=(\operatorname{sh}x\pm\operatorname{ch}x)^2$
5. Формулы кратных углов:
   1. $\operatorname{sh}3x=4\operatorname{sh}^3x+3\operatorname{sh}x$
   2. $\operatorname{ch}3x=4\operatorname{ch}^3x-3\operatorname{ch}x$
   3. $\operatorname{th}3x=\operatorname{th}x\frac{3+\operatorname{th}^2x}{1+3\operatorname{th}^2x}$
   4. $\operatorname{sh}5x=16\operatorname{sh}^5x+20\operatorname{sh}^3x+5\operatorname{sh}x$
   5. $\operatorname{ch}5x=16\operatorname{ch}^5x-20\operatorname{ch}^3x+5\operatorname{ch}x$
   6. $\operatorname{th}5x=\operatorname{th}x\frac{\operatorname{th}^4x+10\operatorname{th}^2x+5}{5\operatorname{th}^4x+10\operatorname{th}^2x+1}$
6. Произведения
   1. $\operatorname{sh}x\,\operatorname{sh}y=\frac{\operatorname{ch}(x+y)-\operatorname{ch}(x-y)}{2}$
   2. $\operatorname{sh}x\,\operatorname{ch}y=\frac{\operatorname{sh}(x+y)+\operatorname{sh}(x-y)}{2}$
   3. $\operatorname{ch}x\,\operatorname{ch}y=\frac{\operatorname{ch}(x+y)+\operatorname{ch}(x-y)}{2}$
   4. $\operatorname{th}x\,\operatorname{th}y=\frac{\operatorname{ch}(x+y)-\operatorname{ch}(x-y)}{\operatorname{ch}(x+y)+\operatorname{ch}(x-y)}$
7. Суммы
   1. $\operatorname{sh}x \pm \operatorname{sh}y=2\operatorname{sh}\frac{x \pm y}{2}\operatorname{ch}\frac{x \mp y}{2}$
   2. $\operatorname{ch}x + \operatorname{ch}y=2\operatorname{ch}\frac{x+y}{2}\operatorname{ch}\frac{x -y}{2}$
   3. $\operatorname{ch}x - \operatorname{ch}y=2\operatorname{sh}\frac{x+y}{2}\operatorname{sh}\frac{x -y}{2}$
   4. $\operatorname{th}x \pm \operatorname{th}y=\frac{\operatorname{sh}(x \pm y)}{\operatorname{ch}x\,\operatorname{ch}y}$
8. Формулы понижения степени
   1. $\operatorname{ch}^2\frac{x}{2} = \frac{\operatorname{ch} x + 1}{2}$
   2. $\operatorname{sh}^2\frac{x}{2} = \frac{\operatorname{ch} x - 1}{2}$
9. Производные:
   1. $(\operatorname{sh}x)^\prime=\operatorname{ch}x$
   2. $(\operatorname{ch}x)^\prime=\operatorname{sh}x$
   3. $(\operatorname{th}x)^\prime=\frac{1}{\operatorname{ch}^2x}$
   4. $\operatorname{sh}x=\int\limits^x_0\operatorname{ch}tdt$
   5. $\operatorname{ch}x=1+\int\limits^x_0\operatorname{sh}tdt$
   6. $\operatorname{th}x=\int\limits^x_0\frac{dt}{\operatorname{ch}^2t}$
10. Интегралы:
    1. $\int\operatorname{sh}x\,dx=\operatorname{ch}x+C$
    2. $\int\operatorname{ch}x\,dx=\operatorname{sh}x+C$
    3. $\int\operatorname{th}x\,dx=\ln\operatorname{ch}x+C$
    4. $\int\frac{1}{\operatorname{ch}^2x}\,dx=\operatorname{th}x+C$
    5. $\int\frac{1}{\operatorname{sh}^2x}\,dx=-\operatorname{cth}x+C$

См. также: Список интегралов от гиперболических функций, Список интегралов от обратных гиперболических функций

Неравенства

Для всех $x\in\R$ выполняется:

1. $0 \le \operatorname{ch}x-1 \le |\operatorname{sh} x| < \operatorname{ch}x$
2. $| \operatorname{th}x | <1$

Разложение в степенные ряды

$\operatorname{sh}\,x=x+\frac{x^3}{3!}+\frac{x^5}{5!}+\frac{x^7}{7!}+\ldots=\sum_{n=0}^\infty\frac{x^{2n+1}}{(2n+1)!}$

$\operatorname{ch}\,x=1+\frac{x^2}{2!}+\frac{x^4}{4!}+\frac{x^6}{6!}+\ldots=\sum_{n=0}^\infty\frac{x^{2n}}{(2n)!}$

$\operatorname{th}\,x=x-\frac{x^3}{3}+\frac{2x^5}{15}-\frac{17x^7}{315}+\ldots=\sum_{n=1}^\infty\frac{2^{2n}(2^{2n}-1)B_{2n}x^{2n-1}}{(2n)!},\quad|x|<\frac{\pi}{2}$

$\operatorname{cth}\,x=\frac{1}{x}+\frac{x}{3}-\frac{x^3}{45}+\frac{2x^5}{945}+\ldots=\frac{1}{x}+\sum_{n=1}^\infty\frac{2^{2n}B_{2n}x^{2n-1}}{(2n)!},\quad0<|x|<\pi$ (Ряд Лорана)

Здесь $B_{2n}$ — числа Бернулли.

Графики

sh(x), ch(x), th(x), cth(x)

sinh, cosh и tanh

csch, sech и coth

Аналитические свойства

Гиперболический синус и гиперболический косинус аналитичны во всей комплексной плоскости, за исключением существенно особой точки на бесконечности. Гиперболический тангенс аналитичен везде, кроме полюсов в точках $z=i\pi(n+1/2)$, где $n$ — целое. Вычеты во всех этих полюсах равны единице. Гиперболический котангенс аналитичен везде, кроме точек $z=i\pi n$, вычеты его в этих полюсах также равны единице.

Обратные гиперболические функции

Основная статья: Обратные гиперболические функции

Читаются ареа… (-синус и т. д.) — от лат. «area» — «площадь».

$\operatorname{Arsh}x=\ln(x+\sqrt{x^2+1})$ — обратный гиперболический синус, гиперболический арксинус, ареасинус: $\operatorname{sh}(\operatorname{Arsh}x)=x.$

$\operatorname{Arch}x=\ln \left( x+\sqrt{x^{2}-1} \right);x\ge 1$ — обратный гиперболический косинус, гиперболический арккосинус, ареакосинус.

$\operatorname{Arth}x=\ln\left(\frac{\sqrt{1-x^2}}{1-x}\right)=\frac{1}{2}\ln\left(\frac{1+x}{1-x}\right)$ — обратный гиперболический тангенс, гиперболический арктангенс, ареатангенс.

$\operatorname{Arcth}x=\ln\left(\frac{\sqrt{x^2-1}}{x-1}\right)=\frac{1}{2}\ln\left(\frac{x+1}{x-1}\right)$ — обратный гиперболический котангенс, гиперболический арккотангенс, ареакотангенс.

$\operatorname{Arsch}x=\pm\ln\left(\frac{1+\sqrt{1-x^2}}{x}\right)$ — обратный гиперболический секанс, гиперболический арксеканс, ареасеканс.

$\operatorname{Arcsch}x=\left\{\begin{array}{l}\ln\left(\frac{1-\sqrt{1+x^2}}{x}\right),\quad x<0 \\ \ln\left(\frac{1+\sqrt{1+x^2}}{x}\right),\quad x>0\end{array}\right.$ — обратный гиперболический косеканс, гиперболический арккосеканс, ареакосеканс.

Графики

arsh(x), arch(x), arth(x), arcth(x)

Связь между некоторыми обратными гиперболическими и обратными тригонометрическими функциями:

$\operatorname{Arsh}x=-i\arcsin(-ix),$

$\operatorname{Arsh}(ix)=i\arcsin x,$

$\arcsin x=-i\operatorname{Arsh}(ix),$

$\arcsin (ix)=-i\operatorname{Arsh}(-x),$

где i — мнимая единица.

Эти функции имеют следующее разложение в ряд:

$\operatorname{Arsh}x=x-\left(\frac{1}{2}\right)\frac{x^3}{3}+\left(\frac{1\cdot3}{2\cdot4}\right)\frac{x^5}{5}-\left(\frac{1\cdot3\cdot5}{2\cdot4\cdot6}\right)\frac{x^7}{7}+\ldots=\sum_{n=0}^\infty\left(\frac{(-1)^n(2n)!}{2^{2n}(n!)^2}\right)\frac{x^{2n+1}}{2n+1},\quad x<1;$

$\operatorname{Arch}x=\ln(2x)-\left(\left(\frac{1}{2}\right)\frac{x^{-2}}{2}+\left(\frac{1\cdot3}{2\cdot4}\right)\frac{x^{-4}}{4}+\left(\frac{1\cdot3\cdot5}{2\cdot4\cdot6}\right)\frac{x^{-6}}{6}+\ldots\right)=\ln(2x)-\sum_{n=1}^\infty\left(\frac{(-1)^n(2n)!}{2^{2n}(n!)^2}\right)\frac{x^{-2n}}{2n},\quad x>1;$

$\operatorname{Arth}x=x+\frac{x^3}{3}+\frac{x^5}{5}+\frac{x^7}{7}+\ldots=\sum_{n=0}^\infty\frac{x^{2n+1}}{2n+1},\quad |x|<1.$

В зарубежной литературе обратные гиперболические функции часто обозначают посредством знака минус первой степени: например, $\operatorname{Arth}\,x$ пишут как $\operatorname{tanh}^{-1}x$ (причём $(\operatorname{tanh}\,x)^{-1}$ обозначает другую функцию — $\operatorname{cth}\,x$), и т. д.

История

Первое появление гиперболических функций историки обнаружили в трудах английского математика Абрахама де Муавра (1707, 1722). Современное определение и обстоятельное их исследование выполнил Винченцо Риккати в 1757 году («Opusculorum», том I), он же предложил их обозначения: sh, ch. Риккати исходил из рассмотрения единичной гиперболы (см. рисунок в разделе #Определение).

Независимое открытие и дальнейшее исследование свойств гиперболических функций было проведено Иоганном Ламбертом (1768), который установил широкий параллелизм формул обычной и гиперболической тригонометрии. Н. И. Лобачевский впоследствии использовал этот параллелизм, пытаясь доказать непротиворечивость неевклидовой геометрии, в которой обычная тригонометрия заменяется на гиперболическую.

В обозначениях гиперболических функций утвердился некоторый разнобой. Например, в Энциклопедии Брокгауза и Эфрона используются обозначения $\operatorname{sinhyp}$, $\operatorname{coshyp}$, в русскоязычной литературе закрепились обозначения $\operatorname{sh}, \operatorname{ch}$, в англоязычной закрепились $\sinh, \cosh$.

Применение

Гиперболические функции часто встречаются при вычислении различных интегралов. Некоторые интегралы от рациональных функций и от функций, содержащих радикалы, довольно просто вычисляются с помощью замен переменных с использованием гиперболических функций.

Аналогично тому, как матрицы вида $\begin{pmatrix}\cos x & \sin x\\ -\sin x & \cos x\end{pmatrix}$ описывают повороты двумерного евклидова пространства, матрицы $\begin{pmatrix}\mathop{\mathrm{ch}}\,x & \mathop{\mathrm{sh}}\,x\\ \mathop{\mathrm{sh}}\,x & \mathop{\mathrm{ch}}\,x\end{pmatrix}$ описывают повороты в простейшем двумерном пространстве Минковского. В связи с этим гиперболические функции часто встречаются в теории относительности.

Однородная веревка или цепочка, свободно подвешенная за свои концы, приобретает форму графика функции $y=a\,\mathop{\mathrm{ch}}\,\frac{x}{a}$ (в связи с чем график гиперболического косинуса иногда называют цепной линией). Это обстоятельство используется при проектировании арок, поскольку форма арки в виде перевёрнутой цепной линии наиболее удачно распределяет нагрузку.

Примечания

Литература

• Бугров Я. С., Никольский С. М. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. — Москва: Наука, 1985. — С. 464.

Ссылки

	Гиперболические функции на Викискладе?

• GonioLab: Интерактивная демонстрация тригонометрических и гиперболических функций на Java Web Start
• БСЭ: Знаки математические
• Обратные тригонометрические и гиперболические функции (англ.)