- Отрезок
-
Отрезком может называться одно из двух близких понятий в геометрии и математическом анализе. Отрезок — множество точек, которое обычно изображается ограниченной частью прямой.
Содержание
Отрезок в геометрии
Отрезок прямой — это множество (часть прямой), состоящее из двух различных точек и всех точек, лежащих между ними. При этом сама точка в геометрии является абстрактным объектом, не имеющим никакой длины и вообще каких-либо измеряемых характеристик. Отрезок прямой, соединяющий две точки
 и
и  (которые называются концами отрезка), обозначается следующим образом —
(которые называются концами отрезка), обозначается следующим образом — ![[A;\;B]](8252f1997fd0deb1570530bd48619046.png) . Если в обозначении отрезка опускаются квадратные скобки, то пишут «отрезок
. Если в обозначении отрезка опускаются квадратные скобки, то пишут «отрезок  ». Любая точка, лежащая между концами отрезка, называется его внутренней точкой. Расстояние между концами отрезка называют его длиной и обозначают как
». Любая точка, лежащая между концами отрезка, называется его внутренней точкой. Расстояние между концами отрезка называют его длиной и обозначают как  .
.Отрезок числовой прямой
Отрезок числовой (координатной) прямой (числовой отрезок, сегмент) — множество вещественных чисел
 , удовлетворяющих неравенству
, удовлетворяющих неравенству  , где заранее заданные вещественные числа
, где заранее заданные вещественные числа  и
и 
 называются концами (граничными точками) отрезка. В противоположность им, остальные числа
называются концами (граничными точками) отрезка. В противоположность им, остальные числа  , удовлетворяющие неравенству
, удовлетворяющие неравенству  , называются внутренними точками отрезка.[1]
, называются внутренними точками отрезка.[1]Отрезок обычно обозначается
![[a, b]](2c3d331bc98b44e71cb2aae9edadca7e.png) :
:![[a,b] = \{ x \in \mathbb{R} \mid a \le x \le b \}](a99792e222feddc748cf9f4335b475eb.png) .
.
Любой отрезок заведомо включён в множество вещественных чисел. Отрезок является замкнутым промежутком.
Число
 называется длиной числового отрезка
называется длиной числового отрезка ![[a, b]](2c3d331bc98b44e71cb2aae9edadca7e.png) .
.Стягивающаяся система сегментов
Система сегментов — это бесконечная последовательность элементов множества отрезков на числовой прямой
![\{[a, b] | a, b \in \R \land a < b\}](beb20d1f402b5c6bdd8ea42778db2d5f.png) .
.Система сегментов обозначается
![\{[a_n, b_n]\}_{n = 1}^{\infty}](00770a93f078b1c2d5b50d41be53b05f.png) . Подразумевается, что каждому натуральному числу
. Подразумевается, что каждому натуральному числу  поставлен в соответствие отрезок
поставлен в соответствие отрезок ![~[a_n, b_n]](020e650634c4724c9c724eff00fa2d73.png) .
.Система сегментов
![\{[a_n, b_n]\}_{n = 1}^{\infty}](00770a93f078b1c2d5b50d41be53b05f.png) называется стягивающейся, если[2]
называется стягивающейся, если[2]- каждый следующий отрезок содержится в предыдущем;
- соответствующая последовательность длин отрезков бесконечно мала.
У любой стягивающейся системы сегментов существует единственная точка, принадлежащая всем сегментам этой системы.
Этот факт следует из свойств монотонной последовательности.
Направленный отрезок
Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки
 и
и  представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, выше указанные направленные отрезки не совпадают. Особого обозначения у направленных отрезков нет — то, что у отрезка важно его направление обычно указывается особо.
представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, выше указанные направленные отрезки не совпадают. Особого обозначения у направленных отрезков нет — то, что у отрезка важно его направление обычно указывается особо.Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.
Примечания
- ↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 53. — 672 с. — ISBN 5-482-00445-7
- ↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 3. Теория пределов // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 68 — 105. — 672 с. — ISBN 5-482-00445-7
См. также
- Интервал
- Промежуток
- Алгоритмы построения отрезка
- Прямая
 Категории:
Категории:- Евклидова геометрия
- Элементарная математика
Wikimedia Foundation. 2010.

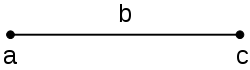
![\forall n \in \N \colon [a_{n+1}, b_{n+1}] \subseteq [a_n, b_n]](6cbed3624c004845f253924f1e81adbb.png)

![\forall \{[a_n, b_n]\}_{n = 1}^{\infty} ~ \exists ! c \in \R ~ \forall n \in N \colon c \in [a_n, b_n]](c90e084238c4ca3157a041d27f59c3b6.png)