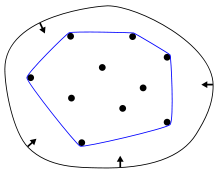
- Выпуклая оболочка
-
Выпуклой оболочкой множества
 называется наименьшее выпуклое множество, содержащее
называется наименьшее выпуклое множество, содержащее  . «Наименьшее множество» здесь означает наименьший элемент по отношению к вложению множеств, то есть такое выпуклое множество, содержащее данную фигуру, что оно содержится в любом другом выпуклом множестве, содержащем данную фигуру.
. «Наименьшее множество» здесь означает наименьший элемент по отношению к вложению множеств, то есть такое выпуклое множество, содержащее данную фигуру, что оно содержится в любом другом выпуклом множестве, содержащем данную фигуру.Обычно выпуклая оболочка определяется для подмножеств векторного пространства над вещественными числами и на соответствующих аффинных пространствах (в частности в евклидовом пространстве).
Выпуклая оболочка множества
 обычно обозначается
обычно обозначается  .
.Содержание
Пример
Представьте себе доску, в которую вбито — но не по самую шляпку — много гвоздей. Возьмите верёвку, свяжите на ней скользящую петлю (лассо) и набросьте её на доску, а потом затяните. Верёвка окружает все гвозди, но касается она только некоторых, самых внешних. Те гвозди, которых она касается, составляют выпуклую оболочку для всей группы гвоздей[1].
Свойства
 — выпуклое множество тогда и только тогда, когда
— выпуклое множество тогда и только тогда, когда  .
.- Для произвольного подмножества линейного пространства
 существует единственная выпуклая оболочка
существует единственная выпуклая оболочка  — это пересечение всех выпуклых множеств, содержащих
— это пересечение всех выпуклых множеств, содержащих  .
.
- При этом
- Более того, если размерность пространства равна
 то верна следующая теорема Каратеодори:
то верна следующая теорема Каратеодори:
- При этом
- Выпуклой оболочкой конечного набора точек на плоскости является выпуклый плоский многоугольник (в вырожденных случаях — отрезок или точка), причём его вершины являются подмножеством исходного набора точек. Аналогичный факт верен и для конечного набора точек во многомерном пространстве.
- Выпуклая оболочка
 равна пересечению всех полупространств, содержащих
равна пересечению всех полупространств, содержащих  .
.
Вариации и обобщения
Выпуклой оболочкой функции f называют такую функцию
 , что
, что ,
,
где epi f — надграфик функции f.
Стоит отметить связь понятия выпуклой оболочки функции с преобразованием Лежандра невыпуклых функций. Пусть f * — преобразование Лежандра функции f. Тогда если
 —собственная функция (принимает конечные значения на непустом множестве), то
—собственная функция (принимает конечные значения на непустом множестве), то
 — выпуклое замыкание f, то есть функция, надграфик которой является замыканием надграфика f.
— выпуклое замыкание f, то есть функция, надграфик которой является замыканием надграфика f.См. также
- Алгоритм Грэхема
- Алгоритм Джарвиса
- Алгоритм Чана
- Выпуклость
- Метод эластичной сети
- Алгоритм быстрой оболочки
- Алгоритм Киркпатрика
Литература
- Половинкин Е. С, Балашов М. В. Элементы выпуклого и сильно выпуклого анализа. — М.: Физматлит, 2004. — 416 с. — ISBN 5-9221-0499-3.
- Прапарата Ф., Шеймос М. Вычислительная геометрия: Введение = Computational Geometry An introduction. — М.: Мир, 1989. — С. 478.
- Кормен, Томас Х., Лейзерсон, Чарльз И., Ривест, Рональд Л., Штайн, Клифорд. Глава 33. Вычислительная геометрия // Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-e издание. — М.: «Вильямс», 2005. — ISBN 5-8459-0857-4
- Ласло М. Вычислительная геометрия и компьютерная графика на C++. — М.: БИНОМ, 1997. — С. 304.
- Ананий В. Левитин Глава 3. Метод грубой силы: Поиск выпуклой оболочки. // Алгоритмы: введение в разработку и анализ = Introduction to The Design and Analysis of Aigorithms. — М.: «Вильямс», 2006. — С. 157-157. — ISBN 0-201-74395-7
Примечания
- ↑ Даниэль Хэльпер, курс «Построение алгоритмов», Хайфский университет.
 Категория:
Категория:- Выпуклая геометрия
Wikimedia Foundation. 2010.