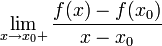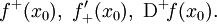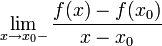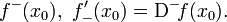- Односторонняя производная
-
В математике существует много различных обобщений понятия производной, так как она является базовой конструкцией дифференциального исчисления.
Односторонние производные
называется правосторо́нней произво́дной или произво́дной спра́ва и обозначается символами
Аналогично, левосторонний предел
называется левосторо́нней произво́дной или произво́дной сле́ва и обозначается символами
Пусть дана функция
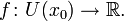 Тогда существует конечная производная f'(x0) тогда и только тогда, когда существуют конечные и равные односторонние производные f' + (x0) = f' − (x0).
Тогда существует конечная производная f'(x0) тогда и только тогда, когда существуют конечные и равные односторонние производные f' + (x0) = f' − (x0).Анализ функций нескольких переменных
Одна из простейших ситуаций, в которых возможно обобщение — это вектор-функции нескольких переменных (наиболее часто область определения представляет собой векторное пространство). Это является предметом изучения анализа функций нескольких переменных.
Частная производная определяется практически идентично производной одиночной вещественной функции, за исключением того, что она распознаёт выбор независимой переменной, который был сделан.
Полная производная функции используется для индикации того, что функция может иметь и явную и неявную зависимость от переменной. Общая производная должна принимать во внимание оба возможных источника изменения, тогда как частная производная должна видеть только явную зависимость.
Производная Лагранжа принимает во внимание изменения вследствие зависимости от времени и движения через пространство по векторному полю.
Для вещественнозначных функций из
 в
в 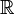 , градиент производит вектор, каждый компонент которого является частной производной. Это может быть использовано для вычисления производных направлений скалярных функций или направлений нормалей.
, градиент производит вектор, каждый компонент которого является частной производной. Это может быть использовано для вычисления производных направлений скалярных функций или направлений нормалей.Для векторнозначных функций
 в
в  , дивергенция (расходимость) даёт меру того, как силён «источник» или «сток» в этой точке. Она может быть использована для вычисления потока при помощи теоремы о дивергенции.
, дивергенция (расходимость) даёт меру того, как силён «источник» или «сток» в этой точке. Она может быть использована для вычисления потока при помощи теоремы о дивергенции.Для векторнозначных функций
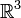 в
в 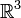 , ротор измеряет «вращение» векторного поля в этой точке.
, ротор измеряет «вращение» векторного поля в этой точке.Для любой функции из
 в
в 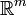 , якобиан — это матрица, содержащая все частные производные всех компонент функции. Без неё невозможно совершить преобразование координат. Её определитель (также называемые якобианом) появляется как множитель при замене переменных в формуле интегрирования.
, якобиан — это матрица, содержащая все частные производные всех компонент функции. Без неё невозможно совершить преобразование координат. Её определитель (также называемые якобианом) появляется как множитель при замене переменных в формуле интегрирования.Производные высшего и дробного порядка
Другое простое обобщение, которое можно произвести, — это применить её больше, чем один раз, получая в результате производную второго (и выше) порядка, как определено в статье о производных. Этот способ может быть обобщён.
В добавок к производным n-ого порядка для любого натурального числа n, используя различные методы, возможно ввести производные в дробных степенях, получая при этом так называемые производные дробного порядка. Производные отрицательных порядков будут соответствовать интегрированию, откуда появляется термин дифферинтеграл. Изучение различных возможных определений и записей производных ненатуральных порядков известно под названием дробное исчисление.
Производные высшего порядка в анализе функций нескольких переменных
Существует несколько различных векторнозначимых и скалярнозначимых производных второго порядка в анализе функций нескольких переменных.
Лапласиан — это дивергенция (расходимость) градиента скалярной функции на
 . Д’Аламбертиан — определяется аналогично лапласиану, но используя неопределённую метрику пространства Минковского, вместо скалярного произведения в евклидовом пространстве
. Д’Аламбертиан — определяется аналогично лапласиану, но используя неопределённую метрику пространства Минковского, вместо скалярного произведения в евклидовом пространстве  .
.Гессианова матрица — это матрица частных производных второго порядка скалярной функции, используемая для вычислений в теории Морса.
Алгебра
Производная в абстрактной алгебре — это линейное отображение на кольце или алгебре, которое удовлетворяет закону Лейбница (правилу произведения). Они изучаются в чистой алгебраической постановке в дифференциальной теории Галуа, но также появляются во многих других областях, где они часто употребляются с менее строгими алгебраическими определениями производных.
Дифференциальная топология
В дифференциальной топологии, векторное поле может быть определено как дифференцирование на кольце гладких функций на многообразии, а касательный вектор может быть определён как производная в точке. Это позволяет абстрагироваться от записи направленной производной скалярной функции и перейти к общим многообразиям. Для многообразий, которые являются подмножествами
 , этот касательный вектор будет аналогичен направленной производной определённой выше.
, этот касательный вектор будет аналогичен направленной производной определённой выше.Пушфорвард отображения между многообразиями — это порождённое отображение между касательными пространствами этих отображений. Оно является абстракцией якобиана.
На внешней алгебре дифференциальных форм над гладким многообразием, внешняя производная это уникальное линейное отображение, которое удовлетворяет порядковой версии закона Лейбница и при возведении в квадрат равно нулю. Это производная 1 порядка на внешней алгебре.
Производная Ли — это скорость изменения одного векторного поля в направлении другого векторного поля. Это пример применения скобки Ли (векторные поля образуют алгебру Ли на группе диффеоморфизмов многообразия). Это производная 0 порядка на алгебре.
Внутренняя производная — это производная «-1» порядка на внешней алгебре форм. Вместе, внешняя производная, производная Ли, и внутренняя производная образуют супералгебру Ли.
Дифференциальная геометрия
В дифференциальной геометрии (и вытекающем из неё тензорном анализе), с помощью ковариантной производной берутся производные по направлениям векторных полей вдоль кривых или вообще в криволинейной системе координат. Это расширяет производную по направлению скалярных функций до сечений векторных расслоений или главных расслоений. В римановой геометрии существование метрики позволяет сделать канонический выбор свободной от кручения ковариантной производной, известной как связность Леви-Чивита.
Внешняя ковариантная производная расширяет внешнюю производную на векторно-значимые формы.
Анализ функций комплексного переменного
В комплексном анализе, центральными объектами изучения являются голоморфные функции, которые являются комплекснозначными функциями на плоскости комплексных чисел и удовлетворяющие соответственно расширенному определению дифференцируемости.
Производная Шварца описывает, как комплексная функция аппроксимируется кусочно-линейным отображением, преимущественно тем же самым способом, каким обычная производная описывает, как функция аппроксимируется линейным отображением.
Функциональный анализ
В функциональном анализе производная Гато расширяет концепцию производной по направлению на локально выпуклые топологические векторные пространства. Производная Фреше позволяет расширить понятие производной на произвольное банахово пространство.
В теории меры производная Радона — Никодима обобщает якобиан, использовавшийся для изменяющихся переменных, на меры. Она выражает одну меру μ в терминах другой меры ν (при некоторых условиях).
Производная также допускает обобщение на пространстве обобщенных функций, используя интегрирование по частям в соответствующем хорошо устроенном подпространстве.
Алгебраическая геометрия
В алгебраической геометрии дифференциал Калера позволяет расширирить определение внешней производной на произвольные алгебраические многообразия, вместо просто гладких многообразий.
Квантовые группы
В области квантовых групп q-производная — это q-деформация обычной производной функции.
Другие обобщения
Вполне можно скомбинировать два или больше различных понятий расширения или абстракции простой производной. Например, в геометрии Финслера изучаются пространства, которые локально выглядят как банаховы пространства. Таким образом можно создать производную с некоторыми особенностями функциональной производной и ковариантной производной.
Нуждающиеся в определении
- Производная Дини
- Производная Гато
- Матричное исчисление
- Производная Пинкерля
- Параметрическая производная
- Полу-дифференцируемость
См. также
Wikimedia Foundation. 2010.