Леви-Чивита Т. — Туллио Леви Чивита (1930 год) Туллио Леви Чивита (итал. Tullio Levi Civita; 29 марта 1873, Падуя, Италия 29 декабря 1941, Рим, Италия) известный итальянский математик еврейского происхождения, знаменитый главным образом своими работами в области… … Википедия
Леви-Чивита Туллио — Туллио Леви Чивита (1930 год) Туллио Леви Чивита (итал. Tullio Levi Civita; 29 марта 1873, Падуя, Италия 29 декабря 1941, Рим, Италия) известный итальянский математик еврейского происхождения, знаменитый главным образом своими работами в области… … Википедия
Леви-Чивита, Туллио — Туллио Леви Чивита (1930 год) Туллио Леви Чивита (итал. Tullio Levi Civita; 29 марта 1873, Падуя, Италия 29 декабря … Википедия
ЛЕВИ-ЧИВИТА СВЯЗНОСТЬ — аффинная связность на римановом пространстве М, к рая является римановой связностью (т. е. связностью, относительно к рой метрич. тензор ковариантно постоянный) и имеет нулевое кручение. Аффинная связность на Мопределяется этими условиями… … Математическая энциклопедия
СВЯЗНОСТЬ — на расслоенном пространстве дифференциально геометрическая структура на гладком расслоенном пространстве со структурной группой Ли, обобщающая связности на многообразии, в частности, напр., Леви Чивита связность в римановой геометрии. Пусть… … Математическая энциклопедия
ЕВКЛИДОВА СВЯЗНОСТЬ — дифференциально геометрическая структура на евклидовом векторном расслоении, обобщающая Леви Чивита связность и риманоеу связность в римановой геометрии. Гладкое векторное расслоение наз. евклидовым, если каждый его слой обладает структурой… … Математическая энциклопедия
КОНФОРМНАЯ СВЯЗНОСТЬ — дифференциально геометрическая структура на гладком многообразии М, специальный вид связности на многообразии, когда приклеенное к Мгладкое расслоенное пространство Еимеет своим типовым слоем конформное пространство С п размерности n=dim M.… … Математическая энциклопедия
ВЕЙЛЯ СВЯЗНОСТЬ — аффинная связность без кручения на римановом пространстве М, обобщающая Леви Чивита связность в том смысле, что ковариант ный дифференциал метрич. тензора пространства Мотносительно нее необязательно, равен нулю, но является пропорциональным… … Математическая энциклопедия
РИМАНОВА СВЯЗНОСТЬ — аффинная связность на римановом пространстве М, относительно к рой метрич. тензор пространства gij является ковариантно постоянным. Если аффинная связность на Мзадана с помощью матрицы локальных форм связности . (1) и метрич. формой на Мявляется … Математическая энциклопедия
АФФИННАЯ СВЯЗНОСТЬ — дифференциально геометрическая структура на гладком многообразии М, специальный вид связности на многообразии, когда приклеенное к Мгладкое расслоенное пространство имеет типовым слоем аффинное пространство размерности . Структурой такого Ек… … Математическая энциклопедия
 на римановом многообразии
на римановом многообразии 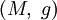 называется связностью Леви-Чивиты, если для неё выполнены следующие два условия:
называется связностью Леви-Чивиты, если для неё выполнены следующие два условия: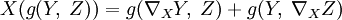 ,
,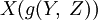 обозначает производную g(Y,Z) в направлении X.
обозначает производную g(Y,Z) в направлении X.![\nabla_XY-\nabla_YX-[X,\;Y]=0](/pictures/wiki/files/97/a255f27dda38f6aafdc8f4d03dd5c32f.png) ,
,![[X,\;Y]](/pictures/wiki/files/102/f3b9ade8a440f424e48b932d8d0671e4.png) скобки Ли векторных полей X и Y.
скобки Ли векторных полей X и Y.