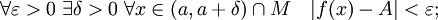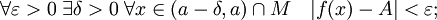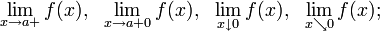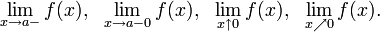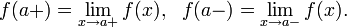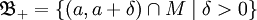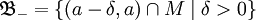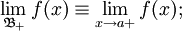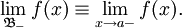- Левосторонний предел
-
Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (или преде́лом спра́ва).
Содержание
Определения
Пусть задана числовая функция
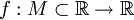 и
и 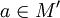 — предельная точка области определения M.
— предельная точка области определения M.- Число
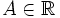 называется правосторонним пределом функции f при x стремящемся к a, если
называется правосторонним пределом функции f при x стремящемся к a, если
- Число
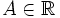 называется левосторонним пределом функции f при x стремящемся к a, если
называется левосторонним пределом функции f при x стремящемся к a, если
Обозначения
- Правосторонний предел принято обозначать любым из нижеследующих способов:
- Аналогичным образом для левосторонних пределов приняты обозначения:
- При этом используются также сокращённые обозначения:
Односторонний предел как предел вдоль фильтра
Односторонний предел является частным случаем общего понятия предела функции вдоль фильтра. Пусть
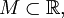 и
и 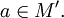 Тогда системы множеств
Тогда системы множестви
являются фильтрами. Пределы вдоль этих фильтров совпадают с соответствующими односторонними пределами:
Свойства
- Основные свойства односторонних пределов идентичны свойствам обычных пределов и являются частными случаями свойств пределов вдоль фильтра.
- Для существования (двустороннего) предела функции необходимо и достаточно, чтобы оба односторонних предела существовали и равнялись между собой.
Примеры
 Функция из Примера 1.
Функция из Примера 1.- Пусть
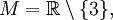 и
и
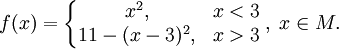
- Тогда (см. рис.)
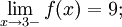
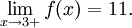
Поскольку односторонние пределы функции f(x) в точке 3 различны, то предела данной функции в 3 не существует.
- Пусть
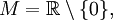 и
и 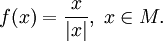 Тогда
Тогда
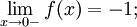
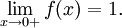
- Опять, поскольку односторонние пределы функции f(x) в точке 0 различны, то предела данной функции в 0 не существует.
См. также
- Число
Wikimedia Foundation. 2010.