- Лапласиан
-
Опера́тор Лапла́са (лапласиа́н) — дифференциальный оператор, действующий в линейном пространстве гладких функций и обозначаемый символом
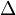 . Функции
. Функции 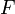 он ставит в соответствие функцию
он ставит в соответствие функцию 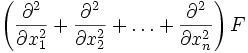 .
.Оператор Лапласа часто обозначается следующим образом
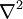 , то есть в виде скалярного произведения оператора Набла на себя. Оператор Лапласа эквивалентен также последовательному взятию операций градиента и дивергенции:
, то есть в виде скалярного произведения оператора Набла на себя. Оператор Лапласа эквивалентен также последовательному взятию операций градиента и дивергенции: 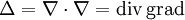 , таким образом значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального векторного поля
, таким образом значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального векторного поля 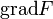 в этой точке.
в этой точке.Содержание
Другое определение оператора Лапласа
Оператор Лапласа является естественным обобщением на функции нескольких переменных обычной второй производной функции одного переменного. В самом деле, если функция
 имеет в окрестности точки
имеет в окрестности точки 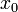 непрерывную вторую производную
непрерывную вторую производную 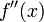 , то, как это следует из формулы Тейлора
, то, как это следует из формулы Тейлора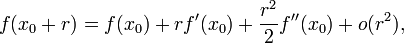 при
при  ,
,
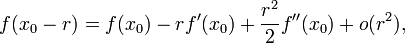 при
при 
вторая производная есть предел
Eсли, переходя к функции
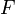 от
от 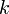 переменных, поступить таким же образом, т.е. для заданной точки
переменных, поступить таким же образом, т.е. для заданной точки 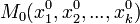 рассматривать её
рассматривать её 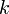 -мерную шаровую окрестность
-мерную шаровую окрестность 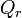 радиуса
радиуса 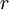 и разность между средним арифметическим
и разность между средним арифметическимфункции
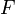 на границе
на границе 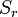 такой окрестности с площадью границы
такой окрестности с площадью границы 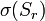 и значением
и значением 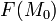 в центре этой окрестности
в центре этой окрестности 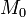 , то в случае непрерывности вторых частных производных функции
, то в случае непрерывности вторых частных производных функции 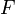 в окрестности точки
в окрестности точки 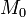 значение лапласиана
значение лапласиана 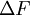 в этой точке есть предел
в этой точке есть пределОдновременно с предыдущим представлением для оператора Лапласа функции
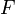 , имеющей непрерывные вторые производные, справедлива формула
, имеющей непрерывные вторые производные, справедлива формула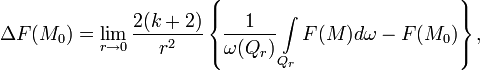 где
где 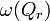 - объём окресности
- объём окресности 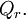
Эта формула выражает непосредственную связь лапласиана функции с её объёмным средним в окрестности данной точки.
Доказательство этих формул можно найти, например, в [1].
Вышеизложенные пределы, во всех случаях, когда они существуют, могут служить определением оператора Лапласа функции
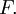 Такое определение предпочтительнее обычного определения лапласиана, предполагающего существование вторых производных рассматриваемых функций, и совпадает с обычным определением в случае непрерывности этих производных.
Такое определение предпочтительнее обычного определения лапласиана, предполагающего существование вторых производных рассматриваемых функций, и совпадает с обычным определением в случае непрерывности этих производных.Выражения для оператора Лапласа в различных криволинейных системах координат
В произвольных ортогональных криволинейных координатах в трехмерном пространстве
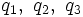 :
: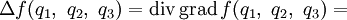
![=\frac{1}{H_1H_2H_3}\left[ \frac{\partial}{\partial q_1}\left( \frac{H_2H_3}{H_1}\frac{\partial f}{\partial q_1} \right) + \frac{\partial}{\partial q_2}\left( \frac{H_1H_3}{H_2}\frac{\partial f}{\partial q_2} \right) + \frac{\partial}{\partial q_3}\left( \frac{H_1H_2}{H_3}\frac{\partial f}{\partial q_3} \right)\right],](/pictures/wiki/files/48/0fc8a2f7852abfc561572a6d358d9391.png)
- где
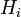 — коэффициенты Ламе.
— коэффициенты Ламе.
Цилиндрические координаты
В цилиндрических координатах вне прямой
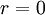 :
:Сферические координаты
В сферических координатах вне начала отсчёта:
или
В случае если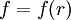
Параболические координаты
В параболических координатах (в трёхмерном пространстве) вне начала отсчёта:
Цилиндрические параболические координаты
В координатах параболического цилиндра вне начала отсчёта:
Применение
С помощью данного оператора удобно записывать уравнения Лапласа, Пуассона и волновое уравнение, хотя наиболее простой вид последнее принимает с использованием оператора Д'Aламбера (Даламбертиана). Впрочем, последний представляет собой не более, чем оператор Лапласа в пространстве Минковского (формально пространство Минковского можно ввести для любого поля, подчиняющегося волновому уравнению, хотя, конечно, параметр c может быть в каждом конкретном случае своим, например, скорость звука).
В физике оператор Лапласа применим в электростатике и электродинамике, во многих уравнениях физики сплошных сред, а также при изучении равновесия мембран, пленок или поверхностей раздела фаз с поверхностным натяжением (см. Лапласово давление), стационарных задач диффузии и теплопроводности, которые сводятся в непрерывном пределе к обычным уравнениям Лапласа или Пуассона или к некоторым их обобщениям.
Вариации и обобщения
См. также
Литература
- ↑ Тиман А.Ф., Трофимов В.Н. Введение в теорию гармонических функций. М. Наука. 1968г. 208с.
Внешние ссылки
Wikimedia Foundation. 2010.

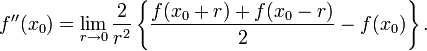
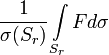
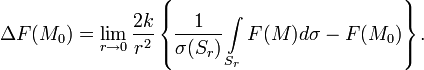
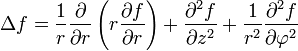
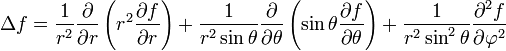
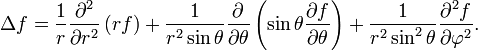
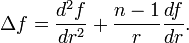
![\Delta f= \frac{1}{\sigma^{2} + \tau^{2}}
\left[
\frac{1}{\sigma} \frac{\partial }{\partial \sigma}
\left( \sigma \frac{\partial f}{\partial \sigma} \right) +
\frac{1}{\tau} \frac{\partial }{\partial \tau}
\left( \tau \frac{\partial f}{\partial \tau} \right)\right] +
\frac{1}{\sigma^2\tau^2}\frac{\partial^2 f}{\partial \varphi^2}](/pictures/wiki/files/55/7e9a6e157bec490dfb0fe18d8bfb05cd.png)
![\Delta F(u,v,z) = \frac{1}{c^2(u^2+v^2)} \left[ \frac{\partial^2 F }{\partial u^2}+ \frac{\partial^2 F }{\partial v^2}\right] + \frac{\partial^2 F }{\partial z^2}](/pictures/wiki/files/97/af2500787981eca027be57cfe66d0ef0.png)