Геометрия Финслера

Финслерова геометрия — метрическое обобщение римановой геометрии, возникающее вслед за введением общего определения длины вектора, не ограниченного частным римановым определением в виде корня квадратного из квадратичной формы.

Определение

Пусть Mⁿ — n-мерное связное 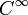$C^{\infty}$-многообразие. Обозначим через TMⁿ касательное расслоение Mⁿ. Тогда финслеровой метрикой на Mⁿ называется функция 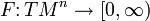$F\colon TM^n\rightarrow [0,\infty)$, удовлетворяющая свойствам:

1. $F\in C^{\infty}(TM^n\setminus\{0\})$;
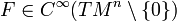2. F положительно однородна первой степени, то есть для любой пары 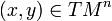$(x,y)\in TM^n$ и числа λ > 0,

   $\ F(x,\lambda y)=\lambda F(x,y)$;

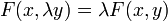3. Для любой пары 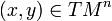$(x,y)\in TM^n$ билинейная форма $\mathbf{g}_y\colon T_x M^n\times T_x M^n\rightarrow \mathbb{R}$,

   $\mathbf{g}_y(u,v)=\frac{1}{2}\frac{\partial^2}{\partial t\,\partial s} \lbrack F^2(x,y+su+tv)\rbrack |_{s=t=0}$

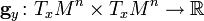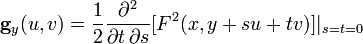
   положительно определена.

История

Идея финслерова пространства восходит к знаменитой лекции Римана «О гипотезах, лежащих в основаниях геометрии» (1854 г.). В этой лекции Риман обсуждает различные возможности метризации n-мерного многообразия и уделяет особое внимание метрике, задаваемой положительным квадратным корнем из положительно определенной квадратичной дифференциальной формы. Эта метрика лежит в основе римановой геометрии. В то же время предполагается, что метрической функцией может служить также и положительный корень четвертой степени из дифференциальной формы четвертого порядка. Указанные метрические функции обладают следующими тремя общими свойствами: они положительны, однородны первой степени по дифференциалам, а также являются выпуклыми функциями дифференциалов. Поэтому представляется естественным ввести дальнейшее обобщение, в котором расстояние между двумя близкими точками определяется некоторой функцией, удовлетворяющей этим трем условиям.

Вызывает удивление, что систематическое изучение многообразий с такой метрикой началось с запозданием более чем на 60 лет. Первым исследованием в этой области стала диссертация Пауля Финслера, увидевшая мир в 1918 г., и поэтому название таких метрических пространств теперь связывают с его именем. Фактором начало исследовательской деятельности в этом направлении, следует, по-видимому, считать введение Каратеодори новых геометрических методов в вариационное исчисление для изучения задач в параметрической форме. Ядром этих методов является понятие индикатрисы, причем свойство выпуклости индикатрисы играет в этих методах важную роль, поскольку оно обеспечивает выполнение необходимых условий минимума в вариационной задаче для стационарных кривых. Именно поэтому диссертация Финслера должна рассматриваться как первый шаг в этом направлении.

Несколькими годами позже в общем развитии финслеровой геометрии происходит интересный поворот от первоначальной точки зрения Финслера к новым теоретическим методам. Финслер, руководствуясь в основном понятиями вариационного исчисления, не использовал методов тензорного анализа. В 1925 тензорный анализ был применен к теории почти одновременно Сингом, Тейлором и Бервальдом.

Новый поворот в развитии теории произошел в 1934 г., когда Э.Картан опубликовал свой трактат о финслеровых пространствах. Картановский подход преобладал практически во всех последующих исследованиях геометрии финслеровых пространств, и несколько математиков выразили мнение, что в результате теория достигла своей окончательной формы. Это мнение, однако, было правильно до некоторой степени. Метод Картана вел к развитию финслеровой геометрии путем прямого развития методов римановой геометрии.

Критику методов Картана независимо друг от друга высказали несколько исследователей, в частности Вагнер, Буземан и Рунд. Ими было подчеркнуто, что естественной локальной метрикой финслерова пространства является метрика Минковского, тогда как произвольное наложение евклидовой метрики затемняет ряд наиболее интересных характеристик финслеровых пространств. По этим причинам в начале 50-х годов были выдвинуты дальнейшие теории. В результате этого заметно увеличились аналитические трудности. Буземан даже сказал по этому поводу, что «Финслерова геометрия со стороны представляет собой лес, в котором вся растительность состоит из тензоров».

В настоящее время значительный вклад в развитие финслеровой геометрии вносит американский математик Шен (англ. Z. Shen). Он написал ряд книг и статей, благодаря которым, вопреки Буземану, изучение финслеровой геометрии становится доступным широкому кругу математиков.

Внешние ссылки

• Сайт Шена о финслеровой геометрии. (англ.)
• Некоммерческий фонд развития исследований по финслеровой геометрии.

Литература

• Х. Рунд Дифференциальная геометрия финслеровых пространств, — М.: «Наука», 1981.
• D. Bao, S.S. Chern and Z. Shen An Introduction to Riemann-Finsler Geometry, — Springer-Verlag, 2000. ISBN 0-387-98948-X.
• S. Chern Finsler geometry is just the Riemannian geometry without the quadratic restriction, — Notices AMS, 43 (1996), pp. 959-63.
• H. Rund The Differential Geometry of Finsler Spaces, — Springer-Verlag, 1959. ASIN B0006AWABG.
• Z. Shen Lectures on Finsler Geometry, — World Scientific Publishers, 2001. ISBN 981-02-4531-9.