- Контравариантный функтор
-
Тео́рия катего́рий — раздел математики, изучающий свойства отношений между математическими объектами, не зависящие от внутренней структуры объектов.
Некоторые математики[кто?] считают теорию категорий слишком абстрактной и непригодной для практического применения. В то же время, теория категорий занимает центральное место в современной математике, она также нашла применения в информатике[1] и в теоретической физике[2][3].
Содержание
Определение
Категория
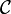 — это:
— это:- класс объектов
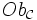 ;
; - для каждой пары объектов A,B задано множество морфизмов (или стрелок)
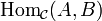 , причём каждому морфизму соответствует единственные A и B;
, причём каждому морфизму соответствует единственные A и B; - для пары морфизмов
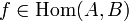 и
и 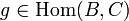 определена композиция
определена композиция 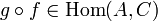 ;
; - для каждого объекта A задан тождественный морфизм
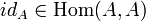 ;
;
причём выполняются две аксиомы:
- операция композиции ассоциативна:
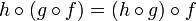 и
и - тождественный морфизм действует тривиально:
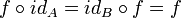 для
для 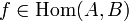
- Замечание: класс объектов обычно не является множеством в смысле аксиоматической теории множеств. Категория, в которой объекты составляют множество, называется малой. Кроме того, в принципе возможно (с небольшим исправлением определения) рассмотрение категорий, в которых морфизмы между любыми двумя объектами также образуют класс, или даже большую структуру[4].
Примеры категорий
- Set — категория множеств. Объектами в этой категории являются множества, морфизмами — отображения множеств.
- Group — категория групп. Объектами являются группы, морфизмами — отображения, сохраняющие групповую структуру.
- VectK — категория векторных пространств над полем K. Морфизмы — линейные отображения.
- Категория модулей.
Аналогично определяются категории для других алгебраических систем.
- Top — категория топологических пространств. Морфизмы — непрерывные отображения.
- Для любого частично упорядоченного множества можно построить малую категорию, объектами которой являются элементы множества, причём между элементами x и y существует единственный морфизм тогда и только тогда, когда x≤y (разумеется, следует отличать эту категорию от категории частично упорядоченных множеств!).
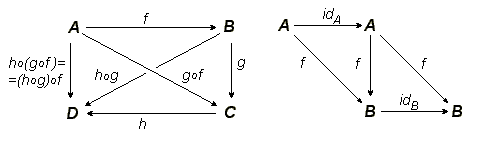
Коммутативные диаграммы
Стандартным способом описания утверждений теории категорий являются коммутативные диаграммы. Коммутативная диаграмма — это ориентированный граф, в вершинах которого находятся объекты, а стрелками являются морфизмы или функторы, причём результат композиции стрелок не зависит от выбранного пути. Например, аксиомы теории категорий можно записать с помощью диаграмм:
Двойственность
Для категории
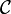 можно определить двойственную категорию
можно определить двойственную категорию 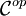 , в которой:
, в которой:- объекты совпадают с объектами исходной категории;
- морфизмы получаются «обращением стрелок»:
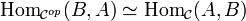
Вообще, для любого утверждения теории категорий можно сформулировать двойственное утверждение с помощью обращения стрелок. Часто двойственное явление обозначается тем же термином с приставкой ко- (см. примеры дальше).
Основные определения и свойства
Изоморфизм, эндоморфизм, автоморфизм
Морфизм
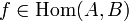 называется изоморфизмом, если существует такой морфизм
называется изоморфизмом, если существует такой морфизм 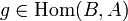 , что
, что 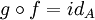 и
и 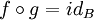 . Два объекта, между которыми существует изоморфизм, называются изоморфными. В частности, тождественный морфизм является изоморфизмом, поэтому любой объект изоморфен сам себе.
. Два объекта, между которыми существует изоморфизм, называются изоморфными. В частности, тождественный морфизм является изоморфизмом, поэтому любой объект изоморфен сам себе.Морфизмы, в которых начало и конец совпадают, называют эндоморфизмами. Множество эндоморфизмов End(A) = Hom(A,A) является моноидом относительно операции композиции с единичным элементом idA.
Эндоморфизмы, которые одновременно являются изоморфизмами, называются автоморфизмами. Автоморфизмы любого объекта образуют группу автоморфизмов Aut(A) по композиции.
Мономорфизм, эпиморфизм, биморфизм
Мономорфизм — это морфизм
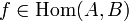 такой, что для любых
такой, что для любых 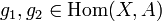 из
из 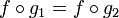 следует, что g1 = g2. Композиция мономорфизмов есть мономорфизм.
следует, что g1 = g2. Композиция мономорфизмов есть мономорфизм.Эпиморфизм — это такой морфизм, что для любых
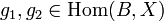 из
из 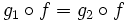 следует g1 = g2.
следует g1 = g2.Биморфизм — это морфизм, являющийся одновременно мономорфизмом и эпиморфизмом. Любой изоморфизм есть биморфизм, но не любой биморфизм есть изоморфизм.
Мономорфизм, эпиморфизм и биморфизм являются обобщениями понятий инъективного, сюръективного и биективного отображения соответственно. Любой изоморфизм является мономорфизмом и эпиморфизмом, обратное, вообще говоря, верно не для всех категорий.
Инициальный и терминальный объекты
Инициальный (начальный, универсально отталкивающий) объект категории — это такой объект, из которого существует единственный морфизм в любой другой объект.
Если инициальные объекты в категории существуют, то все они изоморфны.
Двойственным образом определяется терминальный или универсально притягивающий объект — это такой объект, в который существует единственный морфизм из любого другого объекта.
- Пример: В категории Set инициальным объектом является пустое множество
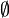 , терминальным — множество из одного элемента
, терминальным — множество из одного элемента 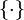 .
. - Пример: В категории Group инициальный и терминальный объект совпадают — это группа из одного элемента.
Произведение и сумма объектов
Произведение объектов A и B — это объект
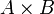 с морфизмами
с морфизмами 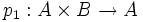 и
и 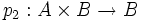 такими, что для любого объекта C с морфизмами
такими, что для любого объекта C с морфизмами 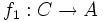 и
и 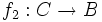 существует единственный морфизм
существует единственный морфизм 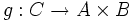 такой, что диаграмма справа коммутативна. Морфизмы
такой, что диаграмма справа коммутативна. Морфизмы 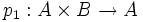 и
и 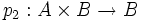 называются проекциями.
называются проекциями.Дуально определяется прямая сумма или копроизведение A + B объектов A и B. Соответствующие морфизмы
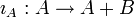 и
и 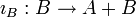 называются вложениями. Несмотря на своё название, в общем случае они могут и не быть мономорфизмами.
называются вложениями. Несмотря на своё название, в общем случае они могут и не быть мономорфизмами.Если произведение и копроизведение существуют, то они определяются однозначно с точностью до изоморфизма.
- Пример: В категории Set прямое произведение A и B — это произведение в смысле теории множеств
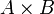 , а прямая сумма — дизъюнктное объединение
, а прямая сумма — дизъюнктное объединение  .
. - Пример: В категории Ring прямая сумма — это тензорное произведение
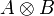 , а прямое произведение — сумма колец
, а прямое произведение — сумма колец 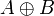 .
. - Пример: В категории VectK прямое произведение и прямая сумма изоморфны — это сумма векторных пространств
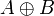 .
.
Функторы
Функторы — это отображения категорий, сохраняющие структуру. Точнее,
(Ковариантный) функтор
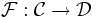 ставит в соответствие каждому объекту категории
ставит в соответствие каждому объекту категории 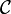 объект категории
объект категории 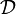 и каждому морфизму
и каждому морфизму 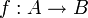 морфизм
морфизм 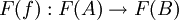 так, что
так, что- F(idA) = idF(A) и
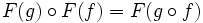 .
.
Контравариантный функтор, или кофунктор — это функтор из
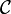 в
в 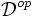 , то есть «функтор, переворачивающий стрелки».
, то есть «функтор, переворачивающий стрелки».Некоторые типы категорий
- Моноидальные категории
- Абелевы категории
- Топосы
См. также
Ссылки
- ↑ D.E. Rydeheard, R.M. Burstall Computational Category Theory, — New York: Prentice Hall. — 1988. — XIII, 257 p. — ISBN 0-13-162736-8.
- ↑ Нужна ли физикам теория категорий?
- ↑ Топосы для физики. (англ.)
- ↑ J. Adámek, H. Herrlich, G. E. Strecker Abstract and concrete categories: The joy of cats, — New York: John Wiley and Sons, — 1990.
Литература
- С. Мак Лейн [Maclane S.] Категории для работающего математика. — М.: Физматлит, 2004 [1998].
- С. Мак Лейн [Maclane S.] Гомология. — М.: Мир — том 114 серии Springer-Verlag — Grundlehren der mathematischen wissenschaften, 1966 [1963].
- Цаленко М. С., Шульгейфер Е. Г. Основы теории категорий. — М.: Наука, 1974.
- Цаленко М. С., Шульгейфер Е. Г. Лекции по теории категорий. — М.: Наука, 1970.
- Цаленко М. С., Шульгейфер Е. Г. Категории. — том 06 серии — ВИНИТИ — Итоги науки и техники, Алгебра-Топология-Геометрия`, 1969.
- Букур [Bucur I.] Деляну[Deleanu A.] Введение в теорию категорий и функторов. — том 19 серии Pure & applied mathematics — a series of texts & monographs — 1972 [1968].
- Фейс [Faith C.] Алгебра — кольца, модули и категории, том 1. — М.: Мир — том 190 серии Springer-Verlag — Grundlehren der mathematischen wissenschaften — 1977 [1973].
- Фейс [Faith C.] Алгебра — кольца, модули и категории, том 2. — М.: Мир — том 191 серии Springer-Verlag — Grundlehren der mathematischen wissenschaften — 1977 [1976].
- Габриель [Gabriel P.], Цисман [Zisman M.] Категории частных и теория гомотопий. — М.: Мир — том 35 серии Springer-Verlag — Ergebnisse der mathematik und ihrer grenzgebiete — 1971 [1967].
- Голдблатт [Goldblatt R.] Топосы — категорный анализ логики. — том 98 серии Studies in logic & foundation of mathematics — 1983 [1979].
- Фултон Е, Мак-Фёрсон Р. Категорный подход к изучению пространств с особенностями. — том 33 серии Новое в зарубежной науке, математика — ред. Бухштабер В. М. — 1983.
- класс объектов
Wikimedia Foundation. 2010.