МНОГОМЕСТНЫЙ ФУНКТОР

мультифунктор,- функция от нескольких аргументов, определенная на категориях, принимающая значения в категории и задающая одноместный функтор по каждому аргументу. Более точно, пусть даны га категорий , Построим декартово произведение категорий где каждая категория либо совпадает с , либо с дуальной категорией Одноместный ковариантный функтор из со значениями в категории наз. n-м естным функтором, заданным на категориях со значениями в категории . Функтор Fковариантен по тем аргументам, к-рые соответствуют множителям в произведении , и контравариантен по остальным аргументам.

Выпишем явно соотношения, к-рым должно удовлетворять отображение (для простоты n=2 и первый аргумент считается контравариантным, а второй - ковариантным). Функтор сопоставляет каждой паре объектов ( А, В), где объект и каждой паре морфизмов , где

морфизм

При этом выполняются следующие условия:

1) для любой пары объектов А, В;

2) если

то

Примеры М. ф.

1) Пусть - категория с конечными произведениями. Тогда произведение побъектов можно рассматривать как re-местный ковариантный по всем аргументам функтор, определенный на декартовой степени (праз) и принимающий значения в 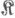. Аналогичные функторы можно построить для ко-произведений, тензорных произведений и т. д.

2) Пусть - произвольная категория. Сопоставим каждой паре объектов А, В из множество морфизмов и каждой паре морфизмов отображение множеств заданное следующим образом:

если

Описанное построение задает двуместный функтор из в категорию множеств, контравариантный по первому аргументу и ковариантный по второму.

Если - аддитивная категория, то можно считать, что построенный функтор принимает значения в категории абелевых групп.

3) Пусть - категория с конечными произведениями. Рассмотрим произведение как двуместный функтор Тогда, комбинируя примеры 1) и 2), можно построить трехместные функторы Первый функтор естественно эквивалентен функтору . В случае категории множеств второй функтор естественно эквивалентен функтору

4) Пусть - малая категория и - категория диаграмм над категорией множеств со схемой , т. е. категория одноместных ковариантных функторов и их естественных преобразований. Построим двуместный ковариантный по обоим аргументам функтор

то ; если - естественное преобразование, то Функтор Еназывают функтором "вычисления значений". Этот функтор естественно эквивалентен функтору к-рый сопоставляет объекту и функтору множество естественных преобразований основного функтора в (лемма Ионеды).