- Инъекция (математика)
-
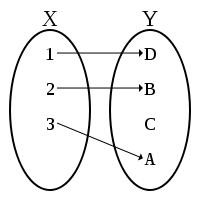
Отображение
 называется инъекцией (или вложением, или отображением «в»), если разные элементы множества
называется инъекцией (или вложением, или отображением «в»), если разные элементы множества  переводятся в разные элементы множества
переводятся в разные элементы множества  .
.Формально это значит, что если два образа совпадают, то совпадают и прообразы (
 ). Инъективность является необходимым условием биективности (достаточно вместе с сюръективностью).
). Инъективность является необходимым условием биективности (достаточно вместе с сюръективностью).Инъекцию можно также определить как отображение, для которого существует левое обратное, то есть,
 инъективно, если существует
инъективно, если существует  , при котором
, при котором  .
.Содержание
Примеры
 — инъективно.
— инъективно. — инъективно.
— инъективно. — не является инъективным (
— не является инъективным ( ).
).
Использование модели
В информатике
Организация связи «один к одному» между таблицами реляционной БД на основе первичных ключей
См. также
Литература
- Н. К. Верещагин, А.Шень. Лекции по математической логике и теории алгоритмов. Часть 1. Начала теории множеств.
- Ершов Ю. Л., Палютин Е. А. Математическая логика: Учебное пособие. — 3-е, стереотип. изд. — СПб.: «Лань», 2004—336 с.
Категории:- Теория множеств
- Типы функций
Wikimedia Foundation. 2010.