Функтор (математика) — У этого термина в программировании есть другое значение: «Функтор (программирование)». Все значения этого слова здесь. Функтор это особый тип отображений между категориями, сохраняющих структуру. Их можно рассматривать как морфизмы в… … Википедия
ГРОТЕНДИКА ГРУППА — аддитивной категории абелева группа, сопоставляемая аддитивной категории универсальным аддитивным отображением. Точнее, пусть С малая аддитивная категория и G абелева группа. Отображение наз. аддитивным, если для любой точной последовательности… … Математическая энциклопедия
КОГОМОЛОГИИ — термин, употребляемый по отношению к функторам гомологической природы, которые, в отличие от гомологии, как правило, контравариантно зависят от объектов основной категории, на которой они определены. В отличие от гомологии, связывающие… … Математическая энциклопедия
МОТИВОВ ТЕОРИЯ — обобщение различных теорий когомологий алгебраич. многообразий. М. т. систематически обобщает идею использования якобиана алгебраич. кривой Xв качестве замены когомологий в классич. теории соответствий и использовании этой теории для изучения… … Математическая энциклопедия
Схема (математика) — В алгебраической геометрии схема это абстракция, позволяющая связать единым образом коммутативную алгебру и дифференциальную геометрию и переносить идеи из одной области в другую. В первую очередь понятие схемы позволяет перенести… … Википедия
РИМАНА - РОХА ТЕОРЕМА — теорема, позволяющая выразить эйлерову характеристику c(Е). локально свободного пучка Ена алгебраическом или аналитич. многообразии Xв терминах характеристич. классов Чжэня пучка Еи многообразия X. Она может быть применена для вычисления… … Математическая энциклопедия
Элементарный топос — См. также: Топос Гротендика В теории категорий элементарный топос это категория, в некотором смысле похожая на категорию множеств. В рамках теории элементарных топосов может быть описана аксиоматика как самой теории множеств, так и… … Википедия
ЛОКАЛИЗАЦИЯ — в категориях специальная конструкция, связанная со .специальными радикальными подкатегориями; она впервые появилась в абелевых категориях для описания т. н. Гротендика категорий с помощью категорий модулей над ассоциативными кольцами с единицей.… … Математическая энциклопедия
ПУЧКОВ ТЕОРИЯ — специальный математич. аппарат, обеспечивающий единый подход для установления связи между локальными и глобальными свойствами топологич. пространств (в частности, геометрич. объектов) и являющийся мощным средством исследования многих задач в… … Математическая энциклопедия
ПИКАРА СХЕМА — естественное обобщение в рамках теории схем понятия Пикара многообразия гладкого алгебраич. многообразий X. Для определения П. с. произвольной S схемы Храссматривается относительный функтор Пикара PicX/S на категории Sch/S схем над схемой S.… … Математическая энциклопедия
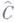 контравариантных функторов, определенных на С и принимающих значения в категории множеств (Ens). Пусть X- объект [U-категории С(где U - фиксированное универсальное множество); сопоставление
контравариантных функторов, определенных на С и принимающих значения в категории множеств (Ens). Пусть X- объект [U-категории С(где U - фиксированное универсальное множество); сопоставление 
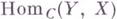 определяет контравариантный функтор
определяет контравариантный функтор  в категорию множеств. Для любого объекта Fкатегории
в категорию множеств. Для любого объекта Fкатегории 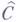 контравариантных функторов из Св категорию (Ens) имеет место естественная биекция
контравариантных функторов из Св категорию (Ens) имеет место естественная биекция 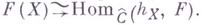 При этом
При этом 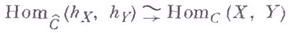
 определяет полное изоморфное вложение
определяет полное изоморфное вложение  , к-рое и наз. Г. ф. С помощью Г. ф. можно вводить алгебраич. структуры на объектах категории (см. Групповой объект категории, Групповая схема).
, к-рое и наз. Г. ф. С помощью Г. ф. можно вводить алгебраич. структуры на объектах категории (см. Групповой объект категории, Групповая схема).