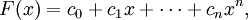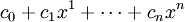- Полиномы
-
В математике, многочлены или полиномы от одной переменной - функции вида
где ci фиксированные коэффициенты, а x — переменная. Многочлены составляют один из важнейших классов элементарных функций.
Изучение полиномиальных уравнений и их решений составляло едва ли не главный объект «классической алгебры». С изучением многочленов связан целый ряд преобразований в математике: введение в рассмотрение нуля, отрицательных, а затем и комплексных чисел, а также появление теории групп как раздела математики и выделение классов специальных функций в анализе.Техническая простота вычислений, связанных с многочленами, по сравнению с более сложными классами функций, а также тот факт, что множество многочленов плотно в пространстве непрерывных функций на компактных подмножествах евклидова пространства (смотри аппроксимационная теорема Вейерштрасса), способствовали развитию методов разложения в ряды и полиномиальной интерполяции в математическом анализе.
Многочлены также играют ключевую роль в алгебраической геометрии, объектом которой являются множества, определённые как решения систем многочленов. Особые свойства преобразования коэффициентов при умножении многочленов используются в алгебраической геометрии, алгебре, теории узлов и других разделах математики для кодирования, или выражения многочленами свойств различных объектов.
Содержание
Определение
Многочлен (или полином) от n переменных — есть конечная формальная сумма вида
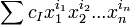 ,
,
где I = (i1,i2,...,in) есть набор из целых неотрицательных чисел (называется мультииндекс), cI — число (называемое «коэффициент многочлена»), зависящее только от мультииндекса I.
В частности, многочлен от одной переменной есть конечная формальная сумма вида
Коэффициенты многочлена обычно берутся из определённого коммутативного кольца R (чаще всего поля, например, поля вещественных или комплексных чисел). В этом случае, относительно операций сложения и умножения многочлены образуют кольцо (более того ассоциативно-коммутативную алгебру над кольцом R без делителей нуля) которое обозначается
- R[x1,x2,...,xn].
Связанные определения
- Многочлен вида
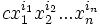 называется одночленом или мономом
называется одночленом или мономом
- Одночлен, соответствующий мультииндексу
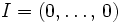 называется свободным членом.
называется свободным членом. - В случае, когда многочлен имеет всего два ненулевых члена, его называют двучленом или биномом,
- В случае, когда многочлен имеет всего три ненулевых члена, его называют трёхчленом.
- Одночлен, соответствующий мультииндексу
- Полной степенью (ненулевого) одночлена
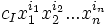 называется целое число | I | = i1 + i2 + ... + in.
называется целое число | I | = i1 + i2 + ... + in.
- Степенью многочлена называется максимальная из степеней его одночленов, тождественный нуль не имеет степени
- Множество мультииндексов I для которых коэффициенты cI ненулевые называется носителем многочлена, а его выпуклая оболочка многогранником Ньютона.
Делимость
Многочлен, который можно представить в виде произведения многочленов низших степеней с коэффициентами из данного поля, называется приводимым (над данным полем), в противном случае — неприводимым. Неприводимые многочлены играют в кольце многочленов роль, сходную с ролью простых чисел в кольце целых чисел. Например, верна теорема: если произведение pq делится на неприводимый многочлен λ, то p или q делится на λ. Каждый многочлен, степени большей нуля, разлагается в данном поле в произведение неприводимых множителей единственным образом (с точностью до множителей нулевой степени).
Например, многочлен x4 + 2, неприводимый в поле рациональных чисел, разлагается на два множителя в поле вещественных чисел и на четыре множителя в поле комплексных чисел.
Вообще, каждый многочлен от одного переменного x разлагается в поле вещественных чисел на множители первой и второй степени, в поле комплексных чисел — на множители первой степени (основная теорема алгебры).
Для двух и большего числа переменных этого уже нельзя утверждать. Над любым полем для любого n > 2 существуют многочлен от n переменных, неприводимые в любом расширении этого поля. Такие многочлены называются абсолютно неприводимыми.
Полиномиальные функции
Пусть A есть алгебра над кольцом R. Произвольный многочлен
![p(x)\in R[x_1,x_2,\dots,x_n]](/pictures/wiki/files/101/e9f417dcd1b29b0e22f190644e824dc6.png) определяет полиномиальную функцию
определяет полиномиальную функцию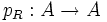 .
.
Чаще всего рассматривают случай A = R.
В случае если R есть поле вещественных или комплексных чисел (а также любое другое поле с бесконечным числом элементов) то функция
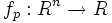 полностью определяет многочлен p. Однако в общем случае это неверно, например: многочлены
полностью определяет многочлен p. Однако в общем случае это неверно, например: многочлены 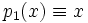 и
и 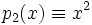 из
из ![\Z_2[x]](/pictures/wiki/files/56/882d3e0463e56562452bb334bf02135f.png) определяют тождественно равные функции
определяют тождественно равные функции 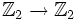 .
.Свойства
- Кольцо многочленов над произвольной областью целостности само является областью целостности.
- Кольцо многочленов от любого конечного числа переменных над любым факториальным кольцом само является факториальным.
- Кольцо многочленов от одного переменного над полем является кольцом главных идеалов, т. е. любой его идеал может быть порожден одним элементом.
- Более того, кольцо многочленов от одного переменного над полем является евклидовым кольцом.
Вариации и обобщения
- Если в определении допустить также отрицательные степени, то полученный объект называется многочленом Лорана (см. ряд Лорана).
- Квазимногочлен
- Тригонометрический многочлен
См. также
- Бином
- Корень многочлена
- Неприводимый многочлен
- Однородный многочлен
- Ортогональные многочлены
- Многогранник Ньютона
- Многочлен Лагранжа
- Многочлен Тейлора
- Многочлен Гильберта
- Многочлен Эрхарта
- Многочлен Чебышёва
- Многочлен Эрмита
- Симметрический многочлен
- Базис Гребнера
- Сплайн
- Характеристический многочлен
- Теорема Гаусса — Лукаса
- Упорядочивание одночленов
Ссылки
Wikimedia Foundation. 2010.