Полином Эрмита

Многочлены Эрмита — определенного вида последовательность многочленов одной вещественной переменной. Многочлены Эрмита возникают в теории вероятностей, в комбинаторике, физике.

Эти многочлены названы в честь Шарля Эрмита.

Определение

В теории вероятностей полиномы Эрмита обычно определяются выражением:

$H_n(x)=(-1)^n e^{x^2/2}\frac{d^n}{dx^n}e^{-x^2/2}\,\!$;

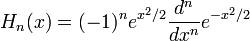в физике обычно используется другое определение:

$H_n(x)=(-1)^n e^{x^2}\frac{d^n}{dx^n}e^{-x^2}\,\!$.

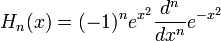Два определения, приведенные выше, не являются в точности эквивалентными друг другу; каждое из них является "отмасштабированной" версией другого

$H_n^\mathrm{phys}(x) = 2^{n/2}H_n^\mathrm{prob}(\sqrt{2}\,x)\,\!$.

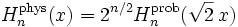Явные выражения для первых десяти многочленов Эрмита приведены ниже (вероятностное определение):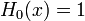

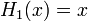
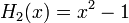
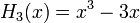
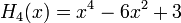
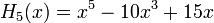
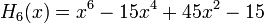
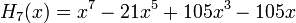
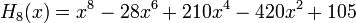
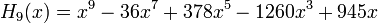
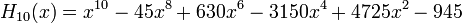$H_0(x)=1\,$

$H_1(x)=x\,$

$H_2(x)=x^2-1\,$

$H_3(x)=x^3-3x\,$

$H_4(x)=x^4-6x^2+3\,$

$H_5(x)=x^5-10x^3+15x\,$

$H_6(x)=x^6-15x^4+45x^2-15\,$

$H_7(x)=x^7-21x^5+105x^3-105x\,$

$H_8(x)=x^8-28x^6+210x^4-420x^2+105\,$

$H_9(x)=x^9-36x^7+378x^5-1260x^3+945x\,$

$H_{10}(x)=x^{10}-45x^8+630x^6-3150x^4+4725x^2-945\,$ .

Свойства

Ортогональность

H_n(x) -- полином порядка n, где n = 0, 1, 2, 3, .... Полиномы этой последовательности попарно ортогональны относительно скалярного произведения, задаваемого выражением:

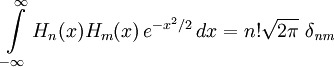$\int\limits_{-\infty}^\infty H_n(x)H_m(x)\,e^{-x^2/2}\,dx=n!\sqrt{2\pi}~\delta_{\mathit{nm}}$ (вероятностная версия)

или

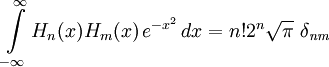$\int\limits_{-\infty}^\infty H_n(x)H_m(x)\,e^{-x^2}\,dx={n!2^n}{\sqrt{\pi}}~\delta_{\mathit{nm}}$ (физическая версия)

где δ_nm -- Символ Кронекера, по определению равный 1, когда n = m и нулю во всех остальных случаях.

Таким образом, многочлены Эрмита образуют отрогональный базис в Гильбертовом пространстве функций, ограниченных в соответствующей норме

$\int\limits_{-\infty}^\infty\left|f(x)\right|^2\,e^{-x^2/2}\,dx<\infty,$.

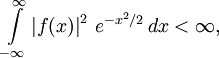Дифференциальное уравнение Эрмита

Многочлен Эрмита n-го порядка удовлетворяет дифференциальному уравнению Эрмита:

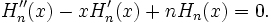$H_n''(x)-xH_n'(x)+nH_n(x)=0.\,\!$ (в теории вероятностей)

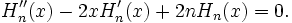$H_n''(x)-2xH_n'(x)+2nH_n(x)=0.\,\!$ (в физике)

Рекурсивное выражение

Последовательность многочленов Эрмита допускает рекурсивное определение:

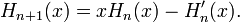$H_{n+1}(x)=xH_n(x)-H_n'(x).\,\!$ (в теории вероятностей)

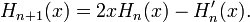$H_{n+1}(x)=2 xH_n(x)-H_n'(x).\,\!$ (в физике)

Применение

1. Полиномы Эрмита применяются, в частности, в методе конечных элементов в качестве функций формы, что позволяет повысить гладкость получаемых приближенных решений.
2. В квантовой механике полиномы Эрмита появляются при решении задачи квантового гармонического осциллятора

Ссылки

• Weisstein, Eric W. Hermite Polynomial на сайте Wolfram MathWorld.(англ.)
• Module for Hermite Polynomial Interpolation by John H. Mathews