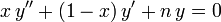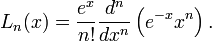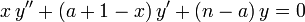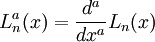ЛАГЕРРА ФУНКЦИИ — ф ции, являющиеся решениями ур ния где , п произвольные параметры. Если п целое положит. число, Л. ф. вырождаются в полиномы Лагерра (см. Ортогональные полиномы). В общем случае Л. ф. выражаются через вырожденную гипергеометрическую функцию … Физическая энциклопедия
Полиномы Лагерра — В математике, Многочлены Лагерра, названные в честь Эдмонда Лагерра (1834 1886), являются каноническими решениями Уравнения Лагерра: являющегося линейным дифференциальным уравнением второго порядка. Это уравнение имеет несингулярное решение… … Википедия
ОРТОГОНАЛЬНЫЕ ПОЛИНОМЫ — системыполиномов , п =0, 1, ..., ортогональных с весом на интервале ( а, b): где квадрат нормы. Подобные системы возникают в разл. задачах матем. физики:в теории представлений групп, в вычислит. математике, при решении задачна собственные… … Физическая энциклопедия
Многочлены Лагерра — В математике, Многочлены Лагерра, названные в честь Эдмона Лагерра (1834 1886), являются каноническими решениями Уравнения Лагерра: являющегося линейным дифференциальным уравнением второго порядка. Многочлены Лагерра также используются в… … Википедия
Обобщенные полиномы Лагерра — В математике, Многочлены Лагерра, названные в честь Эдмонда Лагерра (1834 1886), являются каноническими решениями Уравнения Лагерра: являющегося линейным дифференциальным уравнением второго порядка. Это уравнение имеет несингулярное решение… … Википедия
Обобщённые полиномы Лагерра — В математике, Многочлены Лагерра, названные в честь Эдмонда Лагерра (1834 1886), являются каноническими решениями Уравнения Лагерра: являющегося линейным дифференциальным уравнением второго порядка. Это уравнение имеет несингулярное решение… … Википедия
СПЕЦИАЛЬНЫЕ ФУНКЦИИ — отдельные классы функций, возникающих вомногих теоретич. и прикладных задачах, обычно при решении дифференц. ур ний … Физическая энциклопедия
ИНТЕГРАЛЬНЫЕ ФУНКЦИИ — неск. связанных между собой спец. ф ций, родственных ф ций второго рода Q0(z), определяемых с помощью интегралов от элементарных ф ций (интегральные экспоненты, синус, косинус и логарифм, интегралы вероятности и Френеля). Впервые введены Л.… … Физическая энциклопедия
КЛАССИЧЕСКИЕ ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ — общее название Якоби многочленов, Эрмита многочленов, Лагерра многочленов и Чебышева многочленов. Эти системы ортогональных многочленов обладают общими свойствами: 1) Весовая функция j(х)на интервале ортогональности ( а, b )удовлетворяет… … Математическая энциклопедия
ОРТОГОНАЛЬНЫЕ МНОГОЧЛЕНЫ — система многочленов {Р n (х)}, удовлетворяющих условию ортогональности причем степень каждого многочлена Р n (х). равна его индексу п, а весовая функция (вес) на интервале ( а, b).или (в случае конечности a и b) на отрезке [a, b]. О. м. наз. о р… … Математическая энциклопедия
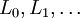 , являются последовательностью полиномов, которая может быть найдена по Формуле Родригеса
, являются последовательностью полиномов, которая может быть найдена по Формуле Родригеса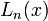
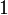
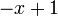
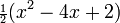
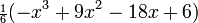
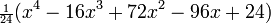
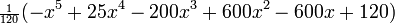
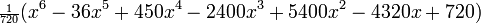
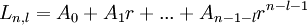
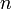 — главное (орбитальное) квантовое число;
— главное (орбитальное) квантовое число;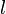 — орбитальное (азимутальное) квантовое число.
— орбитальное (азимутальное) квантовое число.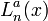 являются решениями уравнения:
являются решениями уравнения: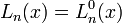 .
.