- Метод Ньютона
-
Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) — это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путём построения последовательных приближений и основан на принципах простой итерации. Метод обладает квадратичной сходимостью. Улучшением метода является метод хорд и касательных. Также метод Ньютона может быть использован для решения задач оптимизации, в которых требуется определить нуль первой производной либо градиента в случае многомерного пространства.
Содержание
Описание метода
Обоснование
Чтобы численно решить уравнение
 методом простой итерации, его необходимо привести к следующей форме:
методом простой итерации, его необходимо привести к следующей форме:  , где
, где  — сжимающее отображение.
— сжимающее отображение.Для наилучшей сходимости метода в точке очередного приближения
 должно выполняться условие
должно выполняться условие  . Решение данного уравнения ищут в виде
. Решение данного уравнения ищут в виде  , тогда:
, тогда:В предположении, что точка приближения «достаточно близка» к корню
 , и что заданная функция непрерывна
, и что заданная функция непрерывна  , окончательная формула для
, окончательная формула для  такова:
такова:С учётом этого функция
 определяется выражением:
определяется выражением:Эта функция в окрестности корня осуществляет сжимающее отображение[1], и алгоритм нахождения численного решения уравнения
 сводится к итерационной процедуре вычисления:
сводится к итерационной процедуре вычисления:По теореме Банаха последовательность приближений стремится к корню уравнения
 .
.Геометрическая интерпретация
Основная идея метода заключается в следующем: задаётся начальное приближение вблизи предположительного корня, после чего строится касательная к исследуемой функции в точке приближения, для которой находится пересечение с осью абсцисс. Эта точка и берётся в качестве следующего приближения. И так далее, пока не будет достигнута необходимая точность.
Пусть
![f(x)\colon[a,\;b]\to\R\!](ca560f1b2661bb38ccc655ef7e8c0480.png) — определённая на отрезке
— определённая на отрезке ![[a,\;b]](186c5c676bac5b18c4105688c2eb69d2.png) и дифференцируемая на нём вещественнозначная функция. Тогда формула итеративного исчисления приближений может быть выведена следующим образом:
и дифференцируемая на нём вещественнозначная функция. Тогда формула итеративного исчисления приближений может быть выведена следующим образом:где
 — угол наклона касательной в точке
— угол наклона касательной в точке  .
.Следовательно искомое выражение для
 имеет вид:
имеет вид:Итерационный процесс начинается с некоего начального приближения
 (чем ближе к нулю, тем лучше, но если предположения о нахождении решения отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях).
(чем ближе к нулю, тем лучше, но если предположения о нахождении решения отсутствуют, методом проб и ошибок можно сузить область возможных значений, применив теорему о промежуточных значениях).Алгоритм
- Задается начальное приближение
 .
. - Пока не выполнено условие остановки, в качестве которого можно взять
 или
или  (то есть погрешность в нужных пределах), вычисляют новое приближение:
(то есть погрешность в нужных пределах), вычисляют новое приближение:  .
.
Пример
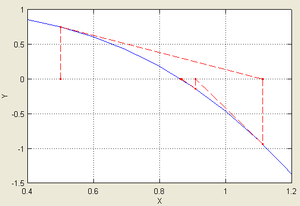
Иллюстрация применения метода Ньютона к функции  с начальным приближением в точке
с начальным приближением в точке  .
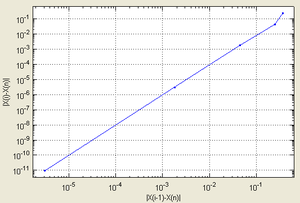
.Согласно способу практического определения скорость сходимости может быть оценена как тангенс угла наклона графика сходимости, то есть в данном случае равна двум. Рассмотрим задачу о нахождении положительных
 , для которых
, для которых  . Эта задача может быть представлена как задача нахождения нуля функции
. Эта задача может быть представлена как задача нахождения нуля функции  . Имеем выражение для производной
. Имеем выражение для производной  . Так как
. Так как  для всех
для всех  и
и  для
для  , очевидно, что решение лежит между 0 и 1. Возьмём в качестве начального приближения значение
, очевидно, что решение лежит между 0 и 1. Возьмём в качестве начального приближения значение  , тогда:
, тогда:Подчёркиванием отмечены верные значащие цифры. Видно, что их количество от шага к шагу растёт (приблизительно удваиваясь с каждым шагом): от 1 к 2, от 2 к 5, от 5 к 10, иллюстрируя квадратичную скорость сходимости.
Условия применения
Рассмотрим ряд примеров, указывающих на недостатки метода.
Контрпримеры
-
- Если начальное приближение недостаточно близко к решению, то метод может не сойтись.
Пусть
Тогда
Возьмём нуль в качестве начального приближения. Первая итерация даст в качестве приближения единицу. В свою очередь, вторая снова даст нуль. Метод зациклится и решение не будет найдено. В общем случае построение последовательности приближений может быть очень запутанным.
-
- Если производная не непрерывна в точке корня, то метод может расходиться в любой окрестности корня.
Рассмотрим функцию:
Тогда
 и
и  всюду, кроме 0.
всюду, кроме 0.В окрестности корня производная меняет знак при приближении
 к нулю справа или слева. В то время, как
к нулю справа или слева. В то время, как  для
для  .
.Таким образом
 не ограничено вблизи корня, и метод будет расходиться, хотя функция всюду дифференцируема, её производная не равна нулю в корне,
не ограничено вблизи корня, и метод будет расходиться, хотя функция всюду дифференцируема, её производная не равна нулю в корне,  бесконечно дифференцируема везде, кроме как в корне, а её производная ограничена в окрестности корня.
бесконечно дифференцируема везде, кроме как в корне, а её производная ограничена в окрестности корня.-
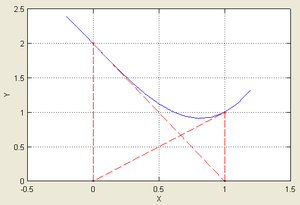
- Если не существует вторая производная в точке корня, то скорость сходимости метода может быть заметно снижена.
Рассмотрим пример:
Тогда
 и
и  за исключением
за исключением  , где она не определена.
, где она не определена.На очередном шаге имеем
 :
:Скорость сходимости полученной последовательности составляет приблизительно 4/3. Это существенно меньше, нежели 2, необходимое для квадратичной сходимости, поэтому в данном случае можно говорить лишь о линейной сходимости, хотя функция всюду непрерывно дифференцируема, производная в корне не равна нулю, и
 бесконечно дифференцируема везде, кроме как в корне.
бесконечно дифференцируема везде, кроме как в корне.-
- Если производная в точке корня равна нулю, то скорость сходимости не будет квадратичной, а сам метод может преждевременно прекратить поиск, и дать неверное для заданной точности приближение.
Пусть
Тогда
 и следовательно
и следовательно  . Таким образом сходимость метода не квадратичная, а линейная, хотя функция всюду бесконечно дифференцируема.
. Таким образом сходимость метода не квадратичная, а линейная, хотя функция всюду бесконечно дифференцируема.Ограничения
Пусть задано уравнение
 , где
, где  и надо найти его решение.
и надо найти его решение.Ниже приведена формулировка основной теоремы, которая позволяет дать чёткие условия применимости. Она носит имя советского математика и экономиста Леонида Витальевича Канторовича (1912—1986).
Теорема Канторовича.
Если существуют такие константы
 , что:
, что: на
на ![[a,\;b]\!](2643171c1e4cfe5eee3b5ea8c1b569be.png) , то есть
, то есть  существует и не равна нулю;
существует и не равна нулю; на
на ![[a,\;b]\!](2643171c1e4cfe5eee3b5ea8c1b569be.png) , то есть
, то есть  ограничена;
ограничена; на
на ![[a,\;b]\!](2643171c1e4cfe5eee3b5ea8c1b569be.png) , и
, и  ;
;
Причём длина рассматриваемого отрезка
 . Тогда справедливы следующие утверждения:
. Тогда справедливы следующие утверждения:- на
![[a,\;b]\!](2643171c1e4cfe5eee3b5ea8c1b569be.png) существует корень
существует корень  уравнения
уравнения ![f(x)=0\colon\exist x^*\in[a,\;b]\colon f(x^*)=0\!](f4c292d21086c1b7f865de68b07240f8.png) ;
; - если
 , то итерационная последовательность сходится к этому корню:
, то итерационная последовательность сходится к этому корню:  ;
; - погрешность может быть оценена по формуле
 .
.
Из последнего из утверждений теоремы в частности следует квадратичная сходимость метода:
Тогда ограничения на исходную функцию
 будут выглядеть так:
будут выглядеть так:- функция должна быть ограничена;
- функция должна быть гладкой, дважды дифференцируемой;
- её первая производная
 равномерно отделена от нуля;
равномерно отделена от нуля; - её вторая производная
 должна быть равномерно ограничена.
должна быть равномерно ограничена.
Историческая справка
Метод был описан Исааком Ньютоном в рукописи «Об анализе уравнениями бесконечных рядов» (лат. «De analysi per aequationes numero terminorum infinitas»), адресованной в 1669 году Барроу, и в работе «Метод флюксий и бесконечные ряды» (лат. «De metodis fluxionum et serierum infinitarum») или «Аналитическая геометрия» (лат. «Geometria analytica») в собраниях трудов Ньютона, которая была написана в 1671 году. В своих работах Ньютон вводит такие понятия, как разложение функции в ряд, бесконечно малые и флюксии (производные в нынешнем понимании). Указанные работы были изданы значительно позднее: первая вышла в свет в 1711 году благодаря Уильяму Джонсону, вторая была издана Джоном Кользоном в 1736 году уже после смерти создателя. Однако описание метода существенно отличалось от его нынешнего изложения: Ньютон применял свой метод исключительно к полиномам. Он вычислял не последовательные приближения
 , а последовательность полиномов и в результате получал приближённое решение
, а последовательность полиномов и в результате получал приближённое решение  .
.Впервые метод был опубликован в трактате «Алгебра» Джона Валлиса в 1685 году, по просьбе которого он был кратко описан самим Ньютоном. В 1690 году Джозеф Рафсон опубликовал упрощённое описание в работе «Общий анализ уравнений» (лат. «Analysis aequationum universalis»). Рафсон рассматривал метод Ньютона как чисто алгебраический и ограничил его применение полиномами, однако при этом он описал метод на основе последовательных приближений
 вместо более трудной для понимания последовательности полиномов, использованной Ньютоном. Наконец, в 1740 году метод Ньютона был описан Томасом Симпсоном как итеративный метод первого порядка решения нелинейных уравнений с использованием производной в том виде, в котором он излагается здесь. В той же публикации Симпсон обобщил метод на случай системы из двух уравнений и отметил, что метод Ньютона также может быть применён для решения задач оптимизации путём нахождения нуля производной или градиента.
вместо более трудной для понимания последовательности полиномов, использованной Ньютоном. Наконец, в 1740 году метод Ньютона был описан Томасом Симпсоном как итеративный метод первого порядка решения нелинейных уравнений с использованием производной в том виде, в котором он излагается здесь. В той же публикации Симпсон обобщил метод на случай системы из двух уравнений и отметил, что метод Ньютона также может быть применён для решения задач оптимизации путём нахождения нуля производной или градиента.В 1879 году Артур Кэли в работе «Проблема комплексных чисел Ньютона — Фурье» (англ. «The Newton-Fourier imaginary problem») был первым, кто отметил трудности в обобщении метода Ньютона на случай мнимых корней полиномов степени выше второй и комплексных начальных приближений. Эта работа открыла путь к изучению теории фракталов.
Обобщения и модификации
Метод одной касательной
В целях уменьшения числа обращений к значениям производной функции применяют так называемый метод одной касательной.
Формула итераций этого метода имеет вид:
Суть метода заключается в том, чтобы вычислять производную лишь один раз, в точке начального приближения
 , а затем использовать это значение на каждой последующей итерации:
, а затем использовать это значение на каждой последующей итерации:При таком выборе
 в точке
в точке  выполнено равенство:
выполнено равенство:и если отрезок, на котором предполагается наличие корня
 и выбрано начальное приближение
и выбрано начальное приближение  , достаточно мал, а производная
, достаточно мал, а производная  непрерывна, то значение
непрерывна, то значение  будет не сильно отличаться от
будет не сильно отличаться от  и, следовательно, график
и, следовательно, график  пройдёт почти горизонтально, пересекая прямую
пройдёт почти горизонтально, пересекая прямую  , что в свою очередь обеспечит быструю сходимость последовательности точек приближений к корню.
, что в свою очередь обеспечит быструю сходимость последовательности точек приближений к корню.Этот метод можно также рассматривать, как модернизацию метода хорд (секущих), где число
 следует выбрать равным
следует выбрать равным 
Многомерный случай
Обобщим полученный результат на многомерный случай.
Пусть необходимо найти решение системы:
Выбирая некоторое начальное значение
![\vec{x}^{[0]}\!](aeda7345eae8d1ec2222d7342be13833.png) , последовательные приближения
, последовательные приближения ![\vec{x}^{[j+1]}\!](558bbc56fe77073b9816ea0ace8345b9.png) находят путём решения систем уравнений:
находят путём решения систем уравнений:где
![\vec{x}^{[j]}=(x_1^{[j]},\;x_2^{[j]},\;\ldots,\;x_n^{[j]}),\quad j=0,\;1,\;2,\;\ldots\!](0eef4d7a7c67eb97cab636c2b7a4a2e8.png) .
.Применительно к задачам оптимизации
Пусть необходимо найти минимум функции многих переменных
 . Эта задача равносильна задаче нахождения нуля градиента
. Эта задача равносильна задаче нахождения нуля градиента  . Применим изложенный выше метод Ньютона:
. Применим изложенный выше метод Ньютона:где
 — гессиан функции
— гессиан функции  .
.В более удобном итеративном виде это выражение выглядит так:
Следует отметить, что в случае квадратичной функции метод Ньютона находит экстремум за одну итерацию.
Нахождение матрицы Гессе связано с большими вычислительными затратами, и зачастую не представляется возможным. В таких случаях альтернативой могут служить квазиньютоновские методы, в которых приближение матрицы Гессе строится в процессе накопления информации о кривизне функции.
Метод Ньютона — Рафсона
Метод Ньютона — Рафсона является улучшением метода Ньютона нахождения экстремума, описанного выше. Основное отличие заключается в том, что на очередной итерации каким-либо из методов одномерной оптимизации выбирается оптимальный шаг:
где
![\lambda_j=\arg\min_\lambda f(\vec{x}^{[j]}-\lambda H^{-1}(\vec{x}^{[j]})\nabla f(\vec{x}^{[j]})).\!](45489d425367214d40e6f6f47a8adef9.png) Для оптимизации вычислений применяют следующее улучшение: вместо того, чтобы на каждой итерации заново вычислять гессиан целевой функции, ограничиваются начальным приближением
Для оптимизации вычислений применяют следующее улучшение: вместо того, чтобы на каждой итерации заново вычислять гессиан целевой функции, ограничиваются начальным приближением ![H(f(\vec{x}^{[0]}))\!](ab7eaadcaf7a860a6f0572b1de9707e6.png) и обновляют его лишь раз в
и обновляют его лишь раз в  шагов, либо не обновляют вовсе.
шагов, либо не обновляют вовсе.Применительно к задачам о наименьших квадратах
На практике часто встречаются задачи, в которых требуется произвести настройку свободных параметров объекта или подогнать математическую модель под реальные данные. В этих случаях появляются задачи о наименьших квадратах:
Эти задачи отличаются особым видом градиента и матрицы Гессе:
где
 — матрица Якоби вектор-функции
— матрица Якоби вектор-функции  ,
,  — матрица Гессе для её компоненты
— матрица Гессе для её компоненты  .
.Тогда очередное направление
 определяется из системы:
определяется из системы:Метод Гаусса — Ньютона
Метод Гаусса — Ньютона строится на предположении о том, что слагаемое
 доминирует над
доминирует над  . Это требование не соблюдается, если минимальные невязки велики, то есть если норма
. Это требование не соблюдается, если минимальные невязки велики, то есть если норма  сравнима с максимальным собственным значением матрицы
сравнима с максимальным собственным значением матрицы  . В противном случае можно записать:
. В противном случае можно записать:Таким образом, когда норма
 близка к нулю, а матрица
близка к нулю, а матрица  имеет полный столбцевой ранг, направление
имеет полный столбцевой ранг, направление  мало отличается от ньютоновского (с учётом
мало отличается от ньютоновского (с учётом  ), и метод может достигать квадратичной скорости сходимости, хотя вторые производные и не учитываются. Улучшением метода является алгоритм Левенберга — Марквардта, основанный на эвристических соображениях.
), и метод может достигать квадратичной скорости сходимости, хотя вторые производные и не учитываются. Улучшением метода является алгоритм Левенберга — Марквардта, основанный на эвристических соображениях.Обобщение на комплексную плоскость
 Бассейны Ньютона для полинома пятой степени
Бассейны Ньютона для полинома пятой степени
 . Разными цветами закрашены области притяжения для разных корней. Более тёмные области соответствуют большему числу итераций.
. Разными цветами закрашены области притяжения для разных корней. Более тёмные области соответствуют большему числу итераций.До сих пор в описании метода использовались функции, осуществляющие отображения в пределах множества вещественных значений. Однако метод может быть применён и для нахождения нуля функции комплексного переменного. При этом процедура остаётся неизменной:
Особый интерес представляет выбор начального приближения
 . Ввиду того, что функция может иметь несколько нулей, в различных случаях метод может сходиться к различным значениям, и вполне естественно возникает желание выяснить, какие области обеспечат сходимость к тому или иному корню. Этот вопрос заинтересовал Артура Кейли ещё в 1879 году, однако разрешить его смогли лишь в 70-х годах двадцатого столетия с появлением вычислительной техники. Оказалось, что на пересечениях этих областей (их принято называть областями притяжения) образуются так называемые фракталы — бесконечные самоподобные геометрические фигуры.
. Ввиду того, что функция может иметь несколько нулей, в различных случаях метод может сходиться к различным значениям, и вполне естественно возникает желание выяснить, какие области обеспечат сходимость к тому или иному корню. Этот вопрос заинтересовал Артура Кейли ещё в 1879 году, однако разрешить его смогли лишь в 70-х годах двадцатого столетия с появлением вычислительной техники. Оказалось, что на пересечениях этих областей (их принято называть областями притяжения) образуются так называемые фракталы — бесконечные самоподобные геометрические фигуры.Ввиду того, что Ньютон применял свой метод исключительно к полиномам, фракталы, образованные в результате такого применения, обрели название фракталов Ньютона или бассейнов Ньютона.
Литература
- Акулич И. Л. Математическое программирование в примерах и задачах: Учеб. пособие для студентов эконом. спец. вузов. — М.: Высш. шк., 1986.
- Амосов А. А., Дубинский Ю. А., Копченова Н. П. Вычислительные методы для инженеров. — М.: Мир, 1998.
- Бахвалов Н. С., Жидков Н. П., Кобельков Г. Г. Численные методы. — 8-е изд.. — М.: Лаборатория Базовых Знаний, 2000.
- Вавилов С. И. Исаак Ньютон. — М.: Изд. АН СССР, 1945.
- Волков Е. А. Численные методы. — М.: Физматлит, 2003.
- Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. — М.: Мир, 1985.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. — М.: Наука, 1970. — С. 575-576.
- Коршунов Ю. М., Коршунов Ю. М. Математические основы кибернетики. — Энергоатомиздат, 1972.
- Максимов Ю. А.,Филлиповская Е. А. Алгоритмы решения задач нелинейного программирования. — М.: МИФИ, 1982.
- Морозов А. Д. Введение в теорию фракталов. — МИФИ, 2002.
Примечания
- ↑ Доказательство: Пусть дана функция вещественного переменного дважды непрерывно дифференцируемая в своей области определения, производная которой нигде не обращается в нуль:
 осуществляет сжимающее отображение вблизи корня уравнения
осуществляет сжимающее отображение вблизи корня уравнения  . В силу непрерывной дифференцируемости функции
. В силу непрерывной дифференцируемости функции  и неравенства нулю её первой производной
и неравенства нулю её первой производной  непрерывна. Производная
непрерывна. Производная  равна:
равна:
 , она также непрерывна. Пусть
, она также непрерывна. Пусть  — искомый корень уравнения:
— искомый корень уравнения:  , следовательно в его окрестности
, следовательно в его окрестности  :
:
 в этой же дельта окрестности выполняется:
в этой же дельта окрестности выполняется:
 в окрестности корня
в окрестности корня  осуществляет сжимающее отображение.
осуществляет сжимающее отображение.
См. также
- Метод простой итерации
- Двоичный поиск
- Метод дихотомии
- Метод секущих
- Метод Мюллера
- Метод хорд
- Фрактал
- Численное решение уравнений
Ссылки
- «Бассейны Ньютона» на сайте fractalworld.xaoc.ru
- «Исаак Ньютон» на сайте www.scottish-wetlands.org
- «Математические работы Канторовича» на сайте Института математики СО РАН
Методы оптимизации Одномерные Метод золотого сечения • Дихотомия • Метод парабол • Перебор по сетке • Метод Фибоначчи • Троичный поиск Прямые методы Метод Гаусса • Метод Нелдера — Мида • Метод Хука — Дживса • Метод конфигураций • Метод Розенброка Первого порядка Градиентный спуск • Метод Зойтендейка • Покоординатный спуск • Метод сопряжённых градиентов • Квазиньютоновские методы • Алгоритм Левенберга — Марквардта Второго порядка Метод Ньютона • Метод Ньютона — Рафсона Стохастические Метод Монте-Карло • Имитация отжига • Эволюционные алгоритмы • Дифференциальная эволюция • Муравьиный алгоритм • Метод роя частиц Методы линейного
программированияСимплекс-метод • Алгоритм Гомори • Метод эллипсоидов • Метод потенциалов Методы нелинейного
программированияПоследовательное квадратичное программирование Категории:- Численные методы
- Алгоритмы оптимизации
Wikimedia Foundation. 2010.





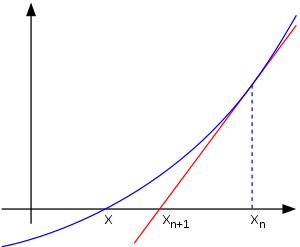
 ). Здесь мы можем увидеть, что последующее приближение
). Здесь мы можем увидеть, что последующее приближение  лучше предыдущего
лучше предыдущего 


 с начальным приближением в точке
с начальным приближением в точке  .
.

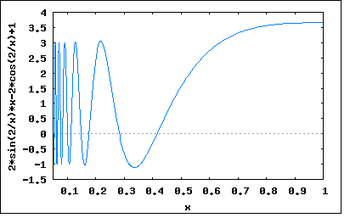
 при приближении
при приближении  к нулю справа.
к нулю справа.




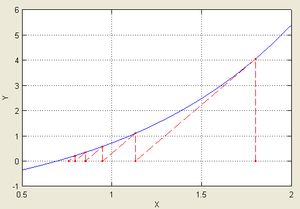
 с начальным приближением в точке
с начальным приближением в точке  .
.



![f_i+\sum_{k=1}^n\frac{\partial f_i}{\partial x_k}(x^{[j+1]}_k-x_k^{[j]})=0,\qquad i=1,\;2,\;\ldots,\;n,\!](90c778e25f4aff9186daf9e557186bb5.png)
![\nabla f(\vec{x}^{[j]})+H(\vec{x}^{[j]})(\vec{x}^{[j+1]}-\vec{x}^{[j]})=0,\quad j=1,\;2,\;\ldots,\;n,\!](de42c54c49e2d933f2d371b5efa48df2.png)
![\vec{x}^{[j+1]}=\vec{x}^{[j]}-H^{-1}(\vec{x}^{[j]})\nabla f(\vec{x}^{[j]}).\!](3aa0196bf8d7518856d5d641bd52c355.png)
![\vec{x}^{[j+1]}=\vec{x}^{[j]}-\lambda_j H^{-1}(\vec{x}^{[j]})\nabla f(\vec{x}^{[j]}),\!](6020b888044d3e66ca51eeb1d7c15eb3.png)



![\left[J^T(\vec{x})J(\vec{x})+\sum_{i=1}^m f_i(\vec{x})H_i(\vec{x})\right]\vec{p}=-J^T(\vec{x})f(\vec{x}).](791c65ac1ac05f785d62d08e59b53af9.png)






