- Теорема Больцано — Коши
-
Теорема Больцано — Коши
Теоре́ма Больца́но — Коши́ о промежуточных значениях непрерывной функции в математическом анализе и общей топологии — это утверждение о том, что если непрерывная функция принимает два значения, то она принимает и любое значение между ними.
Содержание
Формулировка
Пусть дана непрерывная функция на отрезке
![f\in C\bigl([a,b]\bigr).](http://dic.academic.ru/pictures/wiki/files/97/a50cf3e8ab22b5fc3009158720ef0242.png) Пусть также
Пусть также 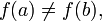 и без ограничения общности предположим, что f(a) = A < B = f(b). Тогда для любого
и без ограничения общности предположим, что f(a) = A < B = f(b). Тогда для любого ![C \in [A,B]](http://dic.academic.ru/pictures/wiki/files/100/d9ad2b8cf55083bea37feafaf3013dcc.png) существует
существует ![c\in [a,b]](http://dic.academic.ru/pictures/wiki/files/48/00a49aece4cc72157b51ca282347a0f8.png) такое, что f(c) = C.Доказательство
такое, что f(c) = C.ДоказательствоРассмотрим функцию
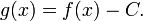 Она непрерывна на отрезке
Она непрерывна на отрезке ![\,[a,b]](http://dic.academic.ru/pictures/wiki/files/98/b66af6dd12e4cb877e42598888762d4f.png) и
и 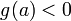 ,
, 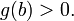 Покажем, что существует такая точка
Покажем, что существует такая точка ![\,c\in [a,b]](http://dic.academic.ru/pictures/wiki/files/52/41b5e90ac58a1a0d000191ba83563b6b.png) , что
, что 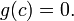 Разделим отрезок
Разделим отрезок ![\,[a,b]](http://dic.academic.ru/pictures/wiki/files/98/b66af6dd12e4cb877e42598888762d4f.png) точкой
точкой 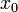 на два равных по длине отрезка, тогда либо
на два равных по длине отрезка, тогда либо 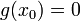 и нужная точка
и нужная точка 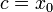 найдена, либо
найдена, либо 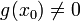 и тогда на концах одного из полученных промежутков функция
и тогда на концах одного из полученных промежутков функция 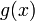 принимает значения разных знаков(на левом конце меньше нуля, на правом больше).
принимает значения разных знаков(на левом конце меньше нуля, на правом больше).Обозначив полученный отрезок
![\,[a_1,b_1]](http://dic.academic.ru/pictures/wiki/files/57/933ee1798fc9962d64c006173193029f.png) , разделим его снова на два равных по длине отрезка и т.д. Тогда, либо через конечное число шагов придем к искомой точке
, разделим его снова на два равных по длине отрезка и т.д. Тогда, либо через конечное число шагов придем к искомой точке  , либо получим последовательность вложенных отрезков
, либо получим последовательность вложенных отрезков ![\,[a_n,b_n]](http://dic.academic.ru/pictures/wiki/files/101/e9c52f22adeabe52200c49e1f322bbfd.png) по длине стремящихся к нулю и таких, что
по длине стремящихся к нулю и таких, что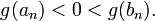
Пусть
 - общая точка всех отрезков
- общая точка всех отрезков ![\,[a_n,b_n]](http://dic.academic.ru/pictures/wiki/files/101/e9c52f22adeabe52200c49e1f322bbfd.png) ,
, 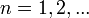 Тогда
Тогда 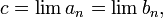 и в силу непрерывности функции
и в силу непрерывности функции 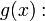
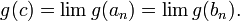
Поскольку
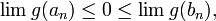
получим, что
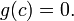
Следствия
- (Теорема о нуле непрерывной функции.) Если функция принимает в концах отрезка положительное и отрицательное значение, то существует точка, в которой она равна нулю. Более точно пусть
![f\in C\bigl([a,b]\bigr),](http://dic.academic.ru/pictures/wiki/files/101/e86f1d165efdacec82a1c5c03daeaa06.png) и f(a),f(b) < 0. Тогда
и f(a),f(b) < 0. Тогда ![\exists c \in [a,b]](http://dic.academic.ru/pictures/wiki/files/57/94db2f38367909e04a2bf303b8cc9aa3.png) такое, что f(c) = 0.
такое, что f(c) = 0. - В частности любой многочлен нечётной степени имеет по меньшей мере один нуль;
Замечание
- Иногда (в учебных курсах) утверждение для нуля называется первой теоремой Больцано — Коши, а общее утверждение — второй теоремой соответственно[1]. На самом деле они эквивалентны.
Обобщение
Теорема Больцано — Коши допускает обобщение на более общие топологические пространства. Всякая непрерывная функция
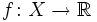 , определенная на линейно связном топологическом пространстве, принимающая какие-либо два значения, принимает и любое лежащее между ними. Более точно пусть дано связное топологическое пространство
, определенная на линейно связном топологическом пространстве, принимающая какие-либо два значения, принимает и любое лежащее между ними. Более точно пусть дано связное топологическое пространство 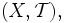 и функция
и функция 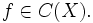 Пусть
Пусть 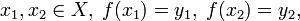 и y1 < y2. Тогда
и y1 < y2. ТогдаВ частности, непрерывный образ линейно связного множества линейно связен.
История
Теорема Больцано — Коши была сформулирована независимо Больцано в 1817 и Коши в 1821.
См. также
Примечания
Литература
Ссылки
Wikimedia Foundation. 2010.
- (Теорема о нуле непрерывной функции.) Если функция принимает в концах отрезка положительное и отрицательное значение, то существует точка, в которой она равна нулю. Более точно пусть
Теорема Больцано — Вейерштрасса — Теорема Больцано Вейерштрасса, или лемма Больцано Вейерштрасса о предельной точке предложение анализа, одна из формулировок которого гласит: из всякой ограниченной последовательности точек пространства можно выделить сходящуюся… … Википедия
Теорема Больцано — Теорема Больцано Вейерштрасса, или лемма Больцано Вейерштрасса о предельной точке предложение анализа, одна из формулировок которого гласит: из всякой ограниченной последовательности точек пространства можно выделить сходящуюся… … Википедия
Теорема Больцано—Коши — … Википедия
Коши, Огюстен — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия
Коши О. — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия
Коши О. Л. — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия
Коши Огюстен Луи — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия
Коши барон — Огюстен Луи Коши Огюстен Луи Коши (фр. Augustin Louis Cauchy; 21 августа 1789, Париж 23 мая 1857, Со (О де Сен)) французский математик, член Парижской академии наук, разработал фундамент математического анализа и сам внёс огромный вклад в анализ … Википедия
Коши, Огюстен Луи — Огюстен Луи Коши Augustin Louis Cauchy … Википедия
Теорема Коши — Теоремой Коши называются следующие утверждения: Интегральная теорема Коши Теорема Коши о многогранниках Теорема Коши о среднем значении Теорема Коши (теория групп) См. также Признак Коши Теорема Больцано Коши Условия Коши Римана … Википедия

![\forall y \in [y_1,y_2]\; \exists x\in X\; f(x) = y.](http://dic.academic.ru/pictures/wiki/files/48/0bd5425f1336513375b30a87ad4cc37d.png)