- Метод хорд
-
Метод хорд — итерационный численный метод приближённого нахождения корня алгебраического уравнения.
Содержание
Геометрическое описание
Будем искать корень функции
 . Выберем две начальные точки
. Выберем две начальные точки  (
( ;
; ) и
) и  (
( ;
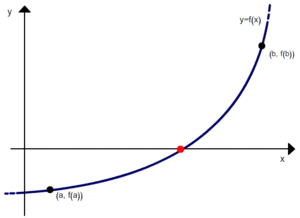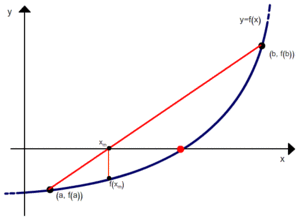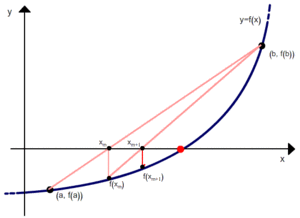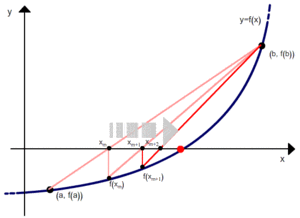
; ) и проведем через них прямую. Она пересечет ось абсцисс в точке (
) и проведем через них прямую. Она пересечет ось абсцисс в точке ( ;0). Теперь найдем значение функции с абсциссой
;0). Теперь найдем значение функции с абсциссой  . Временно будем считать
. Временно будем считать  корнем на отрезке [
корнем на отрезке [ ;
; ]. Пусть точка
]. Пусть точка  имеет абсцисcу
имеет абсцисcу  и лежит на графике. Теперь вместо точек
и лежит на графике. Теперь вместо точек  и
и  мы возьмём точку
мы возьмём точку  и точку
и точку  . Теперь с этими двумя точками проделаем ту же операцию и так далее, то есть будем получать две точки
. Теперь с этими двумя точками проделаем ту же операцию и так далее, то есть будем получать две точки  и
и  и повторять операцию с ними. Отрезок, соединяющий последние 2 точки, пересекает ось абсцисс в точке, значение абсциссы которой можно приближённо считать корнем. Эти действия нужно повторять до тех пор, пока не получим значение корня с нужным приближением.
и повторять операцию с ними. Отрезок, соединяющий последние 2 точки, пересекает ось абсцисс в точке, значение абсциссы которой можно приближённо считать корнем. Эти действия нужно повторять до тех пор, пока не получим значение корня с нужным приближением.Алгебраическое описание метода
Пусть
 − абсциссы концов хорды,
− абсциссы концов хорды,  − уравнение прямой, содержащей хорду. Найдем коэффициенты
− уравнение прямой, содержащей хорду. Найдем коэффициенты  и
и  из системы уравнений:
из системы уравнений: .
.Вычтем из первого уравнения второе:
 , затем найдем коэффициенты
, затем найдем коэффициенты  и
и  :
: , тогда
, тогда .
.Уравнение принимает вид:

Таким образом, теперь можем найти первое приближение к корню, полученное методом хорд:

Теперь возьмем координаты
 и
и  и повторим все проделанные операции, найдя новое приближение к корню. Повторять операцию следует до тех пор, пока
и повторим все проделанные операции, найдя новое приближение к корню. Повторять операцию следует до тех пор, пока  не станет меньше или равно заданному значению погрешности.
не станет меньше или равно заданному значению погрешности.Пример использования
Решим уравнение
 методом хорд. Зададимся точностью ε=0.001 и возьмём в качестве начальных приближений
методом хорд. Зададимся точностью ε=0.001 и возьмём в качестве начальных приближений  и
и  концы отрезка, на котором отделён корень:
концы отрезка, на котором отделён корень:  и
и  , числовые значения
, числовые значения  и
и  выбраны произвольно. Вычисления ведутся до тех пор, пока не выполнится неравенство
выбраны произвольно. Вычисления ведутся до тех пор, пока не выполнится неравенство  .
.Итерационная формула метода хорд имеет вид:
 .
.В нашем примере, в значение
 , подставляется
, подставляется  , а в значение
, а в значение  подставляется
подставляется  . Значение
. Значение  это будет числовое значение
это будет числовое значение  полученное по этой формуле. В дальнейшем
полученное по этой формуле. В дальнейшем  подставляем в формулу в значение
подставляем в формулу в значение  , а
, а  в значение
в значение  .
.По этой формуле последовательно получаем (подчёркнуты верные значащие цифры):
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
Проверим, что метод работает и в том случае, если
 и
и  выбраны по одну и ту же сторону от корня (то есть, если корень не отделён на отрезке между начальными приближениями). Возьмём для того же уравнения
выбраны по одну и ту же сторону от корня (то есть, если корень не отделён на отрезке между начальными приближениями). Возьмём для того же уравнения  и
и  . Тогда:
. Тогда: ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
Мы получили то же значение корня, причём за то же число итераций.
Критерий сходимости
Если
 дважды непрерывно дифференцируемая функция и знак
дважды непрерывно дифференцируемая функция и знак  сохраняется на рассматриваемом промежутке, то полученные приближения будут сходиться к корню монотонно. Если корень
сохраняется на рассматриваемом промежутке, то полученные приближения будут сходиться к корню монотонно. Если корень  уравнения
уравнения  находится на отрезке
находится на отрезке ![~[a,b]](6c65a55c2c8bd6c3e10388d6087e1439.png) , производные
, производные  и
и  на этом промежутке непрерывны и сохраняют постоянные знаки и
на этом промежутке непрерывны и сохраняют постоянные знаки и  , то можно доказать[1], что погрешность приближенного решения стремится к нулю при n→∞, то есть метод сходится и сходится со скоростью геометрической прогрессии (при этом говорят, что он имеет линейную скорость сходимости).
, то можно доказать[1], что погрешность приближенного решения стремится к нулю при n→∞, то есть метод сходится и сходится со скоростью геометрической прогрессии (при этом говорят, что он имеет линейную скорость сходимости).Историческая справка
Первым, кто смог найти приближённые решения кубических уравнений, был Диофант, тем самым заложив основу метода хорд. Сохранившиеся работы Диофанта сообщают об этом. Однако первым, кто понял его методы, был Ферма в XVII веке, а первым, кто дал объяснение методу хорд, был Ньютон (1670-е гг.).[2]
Пример кода
Пример функции вычисления корня методом хорд на отрезке [а; b] на Си/Си++.
double f(double x) { return sqrt(fabs(cos(x))) - x; // Заменить ф-ей, корни которой мы ищем } // a, b - пределы хорды, epsilon - необходимая погрешность double findRoot(double a, double b, double epsilon) { while(fabs(b - a) > epsilon) { a = b - (b - a) * f(b)/(f(b) - f(a)); b = a - (a - b) * f(a)/(f(a) - f(b)); } // a - i-1, b - i-тый члены return b; }
См. также
- Метод Ньютона (метод касательных)
- Метод простой итерации
- Метод секущих
Литература
- Демидович Б.П. и Марон И.А. Основы вычислительной математики. — Наука, 1970. — С. 664.
- Бахвалов, Жидков, Кобельков Численные методы. — Наука. — ISBN 5-94774-060-5
Примечания
Ссылки
Категории:- Численные методы
- Математический анализ
Wikimedia Foundation. 2010.