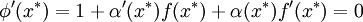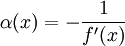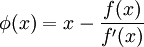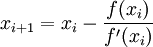- Метод простой итерации
-
Содержание
Постановка задачи
Рассмотрим методы численного решения уравнений и систем уравнений:
или
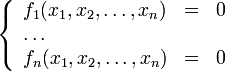
Численное решение задачи можно проводить как непосредственно (используя одноимённые методы), так и с применением оптимизационных методов, приведя задачу к соответствующему виду. Последним посвящена статья Система уравнений и экстремальные задачи. Градиентные методы.
Численные методы решения уравнений
Покажем, как можно решить изначальную систему уравнений, не прибегая к оптимизационным методам. В случае, если наша система представляет собой СЛАУ, целесообразно прибегнуть к таким методам, как метод Гаусса, метод Крамера или метод Ричардсона. Однако мы всё же будем исходить из предположения, что вид функции нам неизвестен и воспользуемся одним из итерационных методов численного решения. Среди большого разнообразия таковых выберем один из наиболее известных — метод Ньютона. Этот метод в свою очередь основывается на принципах метода простой итерации. Поэтому сначала будет изложена суть последнего.
Метод простой итерации
В основе метода заложено понятие сжимающего отображения. Определим терминологию:
Говорят, что функция
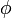 осуществляет сжимающее отображение на
осуществляет сжимающее отображение на ![[a,\; b]\!](/pictures/wiki/files/50/2643171c1e4cfe5eee3b5ea8c1b569be.png) , если
, еслиТогда основная теорема будет выглядеть так:

Теорема Банаха (принцип сжимающих отображений).
Если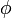 — сжимающее отображение на
— сжимающее отображение на ![[a, \; b]\!](/pictures/wiki/files/50/2643171c1e4cfe5eee3b5ea8c1b569be.png) , то:
, то:
- у
![x=\phi(x)\quad \exist ! x^*\in[a, \; b]\!](/pictures/wiki/files/102/f680e1570bc4274a23ffab716186ce55.png) — корень;
— корень; - итерационная последовательность
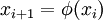 сходится к этому корню;
сходится к этому корню; - для очередного члена
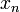 справедливо
справедливо 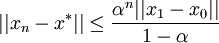 .
.
Поясним смысл параметра
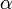 . Согласно теореме Лагранжа имеем:
. Согласно теореме Лагранжа имеем:Отсюда следует, что
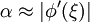 . Таким образом, для сходимости метода достаточно, чтобы
. Таким образом, для сходимости метода достаточно, чтобы ![\forall x \in [a,\; b]\quad |\phi'(x)|\leq 1.\!](/pictures/wiki/files/52/450f2186346e988769c7f2d12e37aef4.png)
Применительно к СЛАУ
Рассмотрим систему:
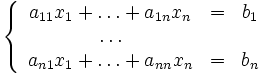
Для неё итерационное вычисление будет выглядеть так:
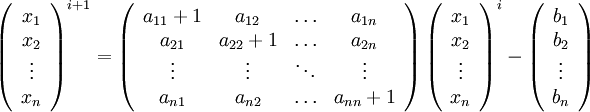
Сходимость методу будет осуществлять
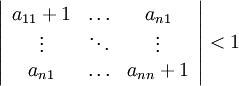
Алгоритм
- Условие
 преобразуется к виду
преобразуется к виду 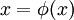 , где
, где 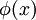 — сжимающая
— сжимающая - Задаётся начальное приближение и точность
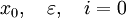
- Вычисляется очередная итерация
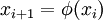
- Если
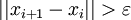 , то
, то 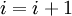 и возврат к шагу 3.
и возврат к шагу 3. - Иначе
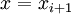 и остановка.
и остановка.
- Если
Метод Ньютона (метод касательных)
Одномерный случай
Для того, чтобы решить уравнение
 , пользуясь методом простой итерации, необходимо привести его к виду
, пользуясь методом простой итерации, необходимо привести его к виду 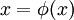 , где
, где 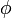 — сжимающее отображение. Чтобы отображение было наиболее эффективно, необходимо, чтобы в точке очередной итерации x * выполнялось
— сжимающее отображение. Чтобы отображение было наиболее эффективно, необходимо, чтобы в точке очередной итерации x * выполнялось 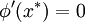 . Будем искать решение данного уравнения в виде
. Будем искать решение данного уравнения в виде 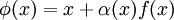 , тогда:
, тогда:Воспользуемся тем, что
 , и получим окончательную формулу для
, и получим окончательную формулу для 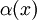 :
:С учётом этого сжимающая функция примет вид:
Тогда алгоритм нахождения численного решения уравнения
 сводится к итерационной процедуре вычисления:
сводится к итерационной процедуре вычисления:Многомерный случай
Обобщим полученный результат на многомерный случай.
Выбирая некоторое начальное приближение
![\vec{x}^{[0]}\!](/pictures/wiki/files/97/aeda7345eae8d1ec2222d7342be13833.png) , находят последовательные приближения
, находят последовательные приближения ![\vec{x}^{[j+1]}\!](/pictures/wiki/files/54/630abb90b61775b45748a0ae7200d721.png) путем решения систем уравнений:
путем решения систем уравнений:![f_i + \sum_{k=1}^n\frac{\partial f_i}{\partial x_k}(x^{[j+1]}_k - x_k^{[j]})=0,\quad i = 1, 2, \ldots, n\!](/pictures/wiki/files/56/85243eb57f67005c5eaab438d3c99243.png) ,
,
где
![x^{[j]}=\left( x_1^{[j]} \ldots x_k^{[j]} \ldots x_n^{[j]} \right), \quad j = 0, 1, 2, \ldots\!](/pictures/wiki/files/102/fccd0360e29faebe74d27d2ebfa894f1.png) .
.Литература
- Амосов А.А., Дубинский Ю. А., Копченова Н.П. Вычислительные методы для инженеров. — М.: Мир, 1998.
- Бахвалов Н.С., Жидков Н.П., Кобельков Г.Г. Численные методы. — 8-е изд.. — М.: Лаборатория Базовых Знаний, 2000.
- Волков Е.А. Численные методы. — М.: Физматлит, 2003.
- Коршунов Ю.М., Коршунов Ю.М. Математические основы кибернетики. — М.: Энергоатомиздат, 1972.
См. также
- Метод Крамера
- Система уравнений и экстремальные задачи. Градиентные методы.
- Теорема Хана-Банаха
- Численные методы
- Метод Гаусса
- Метод Жордана-Гаусса
- Метод обратной матрицы
- Метод Ричардсона
- Метод Чебышева
- Численные методы решения систем линейных уравнений
- Метод итераций
- Метод QR-разложения
- Метод сингулярного разложения
- Метод Зейделя
- Метод релаксации
- Численные методы решения алгебраических и трансцендентных уравнений.
- Метод деления пополам
- Метод хорд
- Метод Ньютона
- Метод секущих
- Комбинированный метод
- Метод итераций
Wikimedia Foundation. 2010.

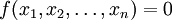
![\forall x \in [ a, \; b ]: \phi(x) \in [a,\; b ]\!](/pictures/wiki/files/50/2f8c4dce6cff179774831b7552b936b4.png)
![\exist \alpha < 1: \forall x_1,x_2 \in [a,\; b ]\quad ||\phi(x_1)-\phi(x_2)||\leq \alpha ||x_1-x_2||\!](/pictures/wiki/files/54/6c6f4066f85de959f081ae1651ee962f.png)
![\phi(x) \in C^1[a, \; b].\quad \forall x_1,x_2 \in (a, \; b),\quad x_1<x_2 \quad \exist \xi \in (x_1,\; x_2): \quad \phi'(\xi)(x_2-x_1) = \phi(x_2)-\phi(x_1)\!](/pictures/wiki/files/98/b194c24c89a7671a8e0aeeb4fe0585cc.png)