- Муравьиный алгоритм
-
Муравьиный алгоритм (алгоритм оптимизации подражанием муравьиной колонии, англ. ant colony optimization, ACO) — один из эффективных полиномиальных алгоритмов для нахождения приближённых решений задачи коммивояжёра, а также аналогичных задач поиска маршрутов на графах. Суть подхода заключается в анализе и использовании модели поведения муравьёв, ищущих пути от колонии к источнику питания и представляет собой метаэвристическую (англ. metaheuristic, meta — «за пределами» и heuristic — «найти») оптимизацию. Первая версия алгоритма, предложенная доктором наук Марко Дориго[1] [2] в 1992 году, была направлена на поиск оптимального пути в графе.
Содержание
История

Хронология алгоритма.
Хронология алгоритмов муравейника:
- 1959 — Пьер-Поль Грассе изложил теорию Stigmergy, чтобы объяснить поведение колонии термитов.[3];
- 1983 — Денеборг и его коллеги проанализировали коллективное поведение муравьёв[4];
- 1988 — Мэйсон и Мандерский опубликовали статью о «само-организации» среди муравьёв[5];
- 1989 — Работа Арона, Госса, Денерборга и Пастелеса «коллективное поведение аргентинских муравьёв», которая дала идею алгоритма муравьиной колонии.[6];
- 1989 — Реализация модели поведения в поисках питания Еблингом и его коллегами[7];
- 1991 — М. Дориго предложил понятие «Муравьиная система» в своей докторской диссертации (которая была опубликована в 1992 году).
- 2001 — IREDA и его сотрудники опубликовали первый многоцелевой алгоритм[8]
- 2002 — Первое применение в разработке графики, Байесовские сети;
- 2002 — Бьянки и ее коллеги предложили первый стохастический алгоритм[9];
- 2004 — Злочин и Дориго показывают, что некоторые алгоритмы эквивалентны: стохастического градиентного спуска, перекрёстной энтропии и алгоритмы для оценки распределения
- 2005 — Первые применения в проблеме сворачивания белка.
Обзор
В основе алгоритма лежит поведение муравьиной колонии — маркировка более удачных путей большим количеством феромона. Работа начинается с размещения муравьёв в вершинах графа (городах), затем начинается движение муравьёв — направление определяется вероятностным методом, на основании формулы вида:
 , где:
, где:  вероятность перехода по пути
вероятность перехода по пути  ,
,  величина, обратная весу (длине)
величина, обратная весу (длине)  -ого перехода,
-ого перехода,  количество феромона на
количество феромона на  -ом переходе,
-ом переходе,  величина, определяющая «жадность» алгоритма,
величина, определяющая «жадность» алгоритма,  величина, определяющая «стадность» алгоритма и
величина, определяющая «стадность» алгоритма и 
Решение не является точным и даже может быть одним из худших, однако, в силу вероятностности решения, повторение алгоритма может выдавать (достаточно) точный результат.
В литературе было предложено несколько метаэвристических моделей ACO. Среди них три наиболее успешные:
- 1) ant system (Dorigo 1992, Dorigo et al. 1991, 1996)
- 2) ant colony system (ACS) (Dorigo & Gambardella 1997)
- 3) MAX-MIN ant system (MMAS) (Stutzle & Hoos 2000)
Краткое изложение
В реальном мире, муравьи (первоначально) ходят в случайном порядке и по нахождению продовольствия возвращаются в свою колонию, прокладывая феромонами тропы. Если другие муравьи находят такие тропы, они, вероятнее всего, пойдут по ним. Вместо того, чтобы отслеживать цепочку, они укрепляют её при возвращении, если в конечном итоге находят источник питания. Со временем феромонная тропа начинает испаряться, тем самым уменьшая свою привлекательную силу. Чем больше времени требуется для прохождения пути до цели и обратно, тем сильнее испарится феромонная тропа. На коротком пути, для сравнения, прохождение будет более быстрым и как следствие, плотность феромонов остаётся высокой. Испарение феромонов также имеет свойство избежания стремления к локально-оптимальному решению. Если бы феромоны не испарялись, то путь, выбранный первым, был бы самым привлекательным. В этом случае, исследования пространственных решений были бы ограниченными. Таким образом, когда один муравей находит (например, короткий) путь от колонии до источника пищи, другие муравьи, скорее всего пойдут по этому пути, и положительные отзывы в конечном итоге приводят всех муравьёв к одному, кратчайшему, пути.
Подробнее
Оригинальная идея исходит от наблюдения за муравьями в процессе поиска кратчайшего пути от колонии до источника питания.
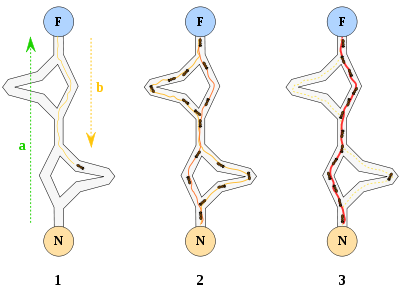
- Первый муравей находит источник пищи (F) любым способом (а), а затем возвращается к гнезду (N), оставив за собой тропу из феромонов (b).
- Затем муравьи выбирают один из четырёх возможных путей, затем укрепляют его и делают привлекательным.
- Муравьи выбирают кратчайший маршрут, так как у более длинных феромоны сильнее испарились.
Среди экспериментов по выбору между двумя путями неравной длины, ведущих от колонии к источнику питания, биологи заметили, что, как правило, муравьи используют кратчайший маршрут.[6] [10] Модель такого поведения заключается в следующем:
- Муравей (так называемый «Блиц») проходит случайным образом от колонии
- Если он находит источник пищи, то возвращается в гнездо, оставляя за собой след из феромона
- Эти феромоны привлекают других муравьёв находящихся вблизи, которые вероятнее всего пойдут по этому маршруту
- Вернувшись в гнездо они укрепят феромонную тропу
- Если существует 2 маршрута, то по более короткому, за то же время, успеют пройти больше муравьёв, чем по длинному
- Короткий маршрут станет более привлекательным
- Длинные пути, в конечном итоге, исчезнут из-за испарения феромонов
Муравьи используют окружающую среду как средство общения. Они обмениваются информацией косвенным путём, через феромоны, в ходе их «работы». Обмен информации имеет локальный характер, только те муравьи, которые находятся в непосредственной близости, где остались феромоны — могут узнать о них. Такая система называется «Stigmergy» и справедлива для многих социальных животных (был изучен в случае строительства столбов в гнёздах термитов). Данный механизм решения проблемы очень сложен и является хорошим примером самоорганизации системы. Такая система базируется на положительной (другие муравьи укрепляют феромонную тропу) и отрицательной (испарение феромонной тропы) обратной связи. Теоретически, если количество феромонов будет оставаться неизменным с течением времени по всем маршрутам, то невозможно будет выбрать путь. Однако из-за обратной связи, небольшие колебания приведут к усилению одного из маршрутов и система стабилизируется к кратчайшему пути.
Вариации алгоритма
Вот одни из самых популярных вариаций муравьиного алгоритма:
Элитарная муравьиная система
MMAS (Max-Min муравьиная система)[11]
Добавляются граничные условия на количество феромонов (τmax,τmin). Феромоны откладываются только на глобально лучших или лучших в итерации путях. Все рёбра инициализируются значением τmax
Пропорциональные псевдослучайные правила
Представлена выше[12]
Ранговая муравьиная система (ASrank)
Все решения ранжируются по степени их пригодности. Количество откладываемых феромонов для каждого решения взвешено так, что более подходящие решения получают больше феромонов, чем менее подходящие.
Длительная ортогональная колония муравьёв (COAC)
Механизм отложения феромонов COAC позволяет муравьям искать решения совместно и эффективно. Используя ортогональный метод, муравьи в выполнимой области могут исследовать их выбранные области быстро и эффективно, с расширенной способностью глобального поиска и точностью.
Ортогональный метод планирования и адаптивный метод регулирования радиуса могут также быть расширены на другие алгоритмы оптимизации для получения более широких преимуществ в решении практических проблем.[13]
Схожесть
Приложение
Пример: псевдо-код и формула
procedure ACO_MetaHeuristic while(not_termination) generateSolutions() daemonActions() pheromoneUpdate() end while end procedureРёбра:
Муравей будет двигаться от узла к узлу
к узлу  с вероятностью:
с вероятностью:
 , где
, где
 — это количество феромонов на ребре
— это количество феромонов на ребре  ;
;  — параметр, контролирующий влияние
— параметр, контролирующий влияние  ;
;  привлекательность ребра
привлекательность ребра  (начальное значение, как правило,
(начальное значение, как правило,  , где d расстояние);
, где d расстояние);  — параметр, контролирующий влияние
— параметр, контролирующий влияние  .
.Обновление феромонов

где
 — количество феромона на дуге
— количество феромона на дуге 
 — скорость испарения феромона
— скорость испарения феромона
 — количество отложенного феромона, обычно определяется как
— количество отложенного феромона, обычно определяется как
где
 — стоимость
— стоимость  -го пути муравья (обычно длина).
-го пути муравья (обычно длина).Другие примеры
Работа-магазин: проблемы планирования
Автомобиль: проблема маршрутизации
Задача о назначениях
Поставленной задачи
Другое
Трудности в определении
Стигмержи алгоритмы
Термин «stigmergy» был введён французским биологом П.-П. Грассе в 1959 году для описания поведения термитов. Он определял его как: «Stimulation of workers by the performance they have achieved.» Термин происходит от двух греческих слов stigma (знак, метка) и ergon (работа, действие).[14]
Похожие методы
См. Роевой интеллект
См. также
Примечания
- ↑ A. Colorni, M. Dorigo et V. Maniezzo, Distributed Optimization by Ant Colonies, actes de la première conférence européenne sur la vie artificielle, Paris, France, Elsevier Publishing, 134—142, 1991.
- ↑ M. Dorigo, Optimization, Learning and Natural Algorithms, PhD thesis, Politecnico di Milano, Italie, 1992.
- ↑ P.-P. Grasse, La reconstruction du nid et les coordinations inter-individuelles chez Belicositermes natalensis et Cubitermes sp. La theorie de la Stigmergie : Essai d’interpretation du comportement des termites constructeurs, Insectes Sociaux, numero 6, p. 41-80, 1959.
- ↑ J.L. Denebourg, J.M. Pasteels et J.C. Verhaeghe, Probabilistic Behaviour in Ants : a Strategy of Errors?, Journal of Theoretical Biology, numero 105, 1983.
- ↑ F. Moyson, B. Manderick, The collective behaviour of Ants : an Example of Self-Organization in Massive Parallelism, Actes de AAAI Spring Symposium on Parallel Models of Intelligence, Stanford, Californie, 1988.
- ↑ 1 2 S. Goss, S. Aron, J.-L. Deneubourg et J.-M. Pasteels, The self-organized exploratory pattern of the Argentine ant, Naturwissenschaften, volume 76, pages 579—581, 1989
- ↑ M. Ebling, M. Di Loreto, M. Presley, F. Wieland, et D. Jefferson,An Ant Foraging Model Implemented on the Time Warp Operating System, Proceedings of the SCS Multiconference on Distributed Simulation, 1989
- ↑ S. Iredi, D. Merkle et M. Middendorf, Bi-Criterion Optimization with Multi Colony Ant Algorithms, Evolutionary Multi-Criterion Optimization, First International Conference (EMO’01), Zurich, Springer Verlag, pages 359—372, 2001.
- ↑ L. Bianchi, L. M. Gambardella et M. Dorigo, An ant colony optimization approach to the probabilistic traveling salesman problem, PPSN-VII, Seventh International Conference on Parallel Problem Solving from Nature, Lecture Notes in Computer Science, Springer Verlag, Berlin, Allemagne, 2002.
- ↑ J.-L. Deneubourg, S. Aron, S. Goss et J.-M. Pasteels, The self-organizing exploratory pattern of the Argentine ant, Journal of Insect Behavior, volume 3, page 159, 1990
- ↑ T. Stützle et H.H. Hoos, MAX MIN Ant System, Future Generation Computer Systems, volume 16, pages 889—914, 2000
- ↑ M. Dorigo et L.M. Gambardella, Ant Colony System : A Cooperative Learning Approach to the Traveling Salesman Problem, IEEE Transactions on Evolutionary Computation, volume 1, numero 1, pages 53-66, 1997.
- ↑ X Hu, J Zhang, and Y Li (2008). Orthogonal methods based ant colony search for solving continuous optimization problems. Journal of Computer Science and Technology, 23(1), pp.2-18.
- ↑ Bonabeau, E. «Editor’s Introduction: Stigmergy.» special Issue of Artificial Life on Stigmergy. Volume 5, Issue 2 / Spring 1999, p.95-96. http://www.stigmergicsystems.com/stig_v1/stigrefs/article1.html
Литература
- M. Dorigo, 1992. Optimization, Learning and Natural Algorithms, PhD thesis, Politecnico di Milano, Italy.
- M. Dorigo, V. Maniezzo & A. Colorni, 1996. «Ant System: Optimization by a Colony of Cooperating Agents», IEEE Transactions on Systems, Man, and Cybernetics-Part B, 26 (1): 29-41.
- M. Dorigo & L. M. Gambardella, 1997. «Ant Colony System: A Cooperative Learning Approach to the Traveling Salesman Problem». IEEE Transactions on Evolutionary Computation, 1 (1): 53-66.
- M. Dorigo, G. Di Caro & L. M. Gambardella, 1999. «Ant Algorithms for Discrete Optimization». Artificial Life, 5 (2): 137—172.
- E. Bonabeau, M. Dorigo et G. Theraulaz, 1999. Swarm Intelligence: From Natural to Artificial Systems, Oxford University Press. ISBN 0-19-513159-2
- M. Dorigo & T. Stützle, 2004. Ant Colony Optimization, MIT Press. ISBN 0-262-04219-3
- M. Dorigo, 2007. «Ant Colony Optimization». Scholarpedia.
- C. Blum, 2005 «Ant colony optimization: Introduction and recent trends». Physics of Life Reviews, 2: 353—373
- M. Dorigo, M. Birattari & T. Stützle, 2006 Ant Colony Optimization: Artificial Ants as a Computational Intelligence Technique. TR/IRIDIA/2006-023
Ссылки
- Оптимизация муравьиной колонии (англ.)
- Муравьиный алгоритм. Библиография
- Ant Colony Optimization Home Page
Методы оптимизации Одномерные Метод золотого сечения • Дихотомия • Метод парабол • Перебор по сетке • Метод Фибоначчи • Троичный поиск Прямые методы Метод Гаусса • Метод Нелдера — Мида • Метод Хука — Дживса • Метод конфигураций • Метод Розенброка Первого порядка Градиентный спуск • Метод Зойтендейка • Покоординатный спуск • Метод сопряжённых градиентов • Квазиньютоновские методы • Алгоритм Левенберга — Марквардта Второго порядка Метод Ньютона • Метод Ньютона — Рафсона Стохастические Метод Монте-Карло • Имитация отжига • Эволюционные алгоритмы • Дифференциальная эволюция • Муравьиный алгоритм • Метод роя частиц Методы линейного
программированияСимплекс-метод • Алгоритм Гомори • Метод эллипсоидов • Метод потенциалов Методы нелинейного
программированияПоследовательное квадратичное программирование Категории:- Алгоритмы оптимизации
- Эволюционные алгоритмы
Wikimedia Foundation. 2010.