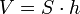- Призма (математика)
-
Призма (математика)
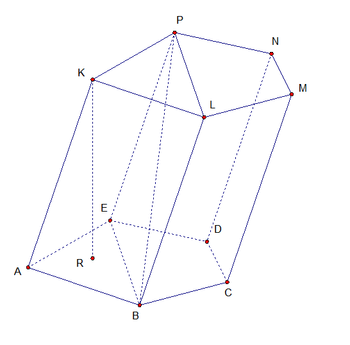
Призма — многогранник, две грани которого являются конгруэнтными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками.
Содержание
Элементы призмы
Название Определение Обозначения на чертеже Чертеж Основания Две грани, являющиеся конгруэнтными многоугольниками, лежащими в параллельных плоскостях. ABCDE, KLMNP Боковые грани Все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. ABLK, BCML, CDNM, DEPN, EAKP Боковая поверхность Объединение боковых граней. Полная поверхность Объединение оснований и боковой поверхности. Боковые ребра Общие стороны боковых граней. AK, BL, CM, DN, EP Высота Отрезок, соединяющий основания призмы и перпендикулярный им. KR Диагональ Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. BP Диагональная плоскость Плоскость, проходящая через боковое ребро призмы и диагональ основания. Диагональное сечение Пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе его частные случаи — ромб, прямоугольник, квадрат. EBLP Перпендикулярное сечение Пересечение призмы и плоскости, перпендикулярной ее боковому ребру. Свойства призмы
- 1. Основания призмы являются равными многоугольниками.
- 2. Боковые грани призмы являются параллелограммами.
- 3. Боковые ребра призмы параллельны и равны.
- 4. Объём призмы равен произведению её высоты на площадь основания:
- 5. Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
Виды призм
Призмы бывают прямые и наклонные.
Прямая призма — призма, у которой все боковые ребра перпендикулярны основанию.
- Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту.
Наклонная призма — призма, у которой хотя бы одно боковое ребро не перпендикулярно основанию.
- Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра.
- Объем наклонной призмы равен произведению площади перпендикулярного сечения на боковое ребро.
Правильная призма — прямая призма, основание которой является правильным многоугольником.
Свойства правильной призмы
- 1. Основания правильной призмы являются правильными многоугольниками.
- 2. Боковые грани правильной призмы являются равными прямоугольниками.
- 3. Боковые ребра правильной призмы равны.
См. также
Ссылки
Многогранники Правильные
(Платоновы тела)Трёхмерные Тетраэдр • Куб • Октаэдр • Додекаэдр • Икосаэдр Четырёхмерные 6 правильных многогранников Большей размерности только 3 типа правильных многогранников: n-мерный симплекс, n-мерный октаэдр, n-мерный куб Правильные невыпуклые Звёздчатый многогранник (Звёздчатый октаэдр, Звёздчатый додекаэдр, Звёздчатый икосаэдр, Звёздчатый икосододекаэдр) Выпуклые Полуправильные многогранники или Архимедовы тела/двойственные многогранники или Каталановы тела
(Кубооктаэдр/Ромбододекаэдр, Икосододекаэдр/Ромботриаконтаэдр, Усечённый тетраэдр/Triakis tetrahedron,
Усечённый куб/Triakis octahedron, Усечённый октаэдр/Tetrakis hexahedron, Усечённый додекаэдр/Triakis icosahedron,
Усечённый икосаэдр/Pentakis dodecahedron, Ромбокубоктаэдр/Дельтоидальный икоситетраэдр,
Ромбоусечённый кубоктаэдр/Disdyakis dodecahedron, Ромбоикосододекаэдр/Дельтоидальный гексеконтаэдр,
Ромбоусечённый икосододекаэдр/Disdyakis triacontahedron,
Курносый куб/Пентагональный икоситетраэдр, Курносый додекаэдр/Пентагональный гексеконтаэдр,
Звёздчатый кубооктаэдр, правильные призма и антипризма)Формулы, теоремы, теории Прочее Группа многогранника • Двенадцатигранники (додекаэдр, пентагондодекаэдр, ромбододекаэдр) • Бипирамида • Зоноэдр • Параллелепипед • Параллелоэдр • Пентагондодекаэдр • Пентеракт • Призматоид • Ромбоэдр • Тессеракт
Wikimedia Foundation. 2010.
Математика в девяти книгах — (начало) «Математика в девяти книгах» (кит. трад. 九章算術 … Википедия
ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
Земляков — Земляков, Александр Николаевич Файл:Zemlyakov.jpg Александр Николаевич Земляков (17 апреля 1950(19500417), Бологое 1 января 2005, Черноголовка) математик,выдающийся советский и российский педагог, автор учебно педагогической… … Википедия
Земляков, Александр Николаевич — Александр Николаевич Земляков (17 апреля 1950(19500417), Бологое 1 января 2005, Черноголовка) математик, выдающийся советский и российский педагог, автор учебно педагогической литературы. Биография Закончил в 1967 году с золотой… … Википедия
Правильный многогранник — Додекаэдр Правильный многогранник или платоново тело это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией … Википедия
Пирамида (геометрия) — У этого термина существуют и другие значения, см. Пирамидацу (значения). Достоверность этого раздела статьи поставлена под сомнение. Необходимо проверить точность фактов, изложенных в этом разделе. На странице обcуждения могут быть пояснения … Википедия
Бипирамида — или дипирамида является трёхмерным многогранником, сформированным из двух пирамид, одна из которых является зеркальным отражением другой. Место соединения пирамид образует общую фигуру в виде многоугольника. Простая бипирамида формируется при… … Википедия
Изгибаемый многогранник — Многогранник (точнее многогранная поверхность) называется изгибаемым, если его пространственную форму можно изменить такой непрерывной во времени деформацией, при которой каждая грань не изменяет своих размеров (то есть движется как твёрдое тело) … Википедия
Норма (философия) — «Мыслитель», Огюст Роден Философия (др. греч. φιλοσοφία «любовь к мудрости», «любомудрие», от φιλέω люблю и σοφία мудрость) наиболее общая теория … Википедия
Определение философии — «Мыслитель», Огюст Роден Философия (др. греч. φιλοσοφία «любовь к мудрости», «любомудрие», от φιλέω люблю и σοφία мудрость) наиболее общая теория … Википедия