Нормальное распределение

Нормальное распределение

Плотность вероятности Зеленая линия соответствует стандартному нормальному распределению
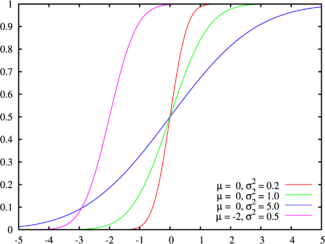
Функция распределения Цвета на этом графике соответствуют графику наверху
Обозначение	$N(\mu,\sigma^2)\,$
Параметры	$\mu$ - коэффициент сдвига (вещественное число) $\sigma>0$ - коэффициент масштаба (вещественный, строго положительный)
Носитель	$x \in (-\infty;+\infty)\!$
Плотность вероятности	$\frac1{\sigma\sqrt{2\pi}}\; \exp\left(-\frac{\left(x-\mu\right)^2}{2\sigma^2} \right) \!$
Функция распределения	$\frac12\Big[1 + \operatorname{erf}\Big( \frac{x-\mu}{\sqrt{2\sigma^2}}\Big)\Big]$
Математическое ожидание	$\mu\,$
Медиана	$\mu\,$
Мода	$\mu\,$
Дисперсия	$\sigma^2\,$
Коэффициент асимметрии	$0\,$
Коэффициент эксцесса	$0\,$
Информационная энтропия	$\ln\left(\sigma\sqrt{2\,\pi\,e}\right)\!$
Производящая функция моментов	$M_X(t)= \exp\left(\mu\,t+\frac{\sigma^2 t^2}{2}\right)$
Характеристическая функция	$\phi_X(t)=\exp\left(\mu\,i\,t-\frac{\sigma^2 t^2}{2}\right)$

Нормальное распределение, также называемое гауссовым распределением, гауссианой или распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:

$f(x) = \tfrac{1}{\sigma\sqrt{2\pi}}\; e^{ -\frac{(x-\mu)^2}{2\sigma^2} },$

где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.

Нормальное распределение играет важнейшую роль во многих областях знаний, особенно в статистической физике. Физическая величина, подверженная влиянию значительного числа независимых факторов, способных вносить с равной погрешностью положительные и отрицательные отклонения, вне зависимости от природы этих случайных факторов, часто подчиняется нормальному распределению, поэтому из всех распределений в природе чаще всего встречается нормальное (отсюда и произошло одно из названий этого распределения вероятностей).

Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.

Свойства

Если случайные величины $X_1$ и $X_2$ независимы и имеют нормальное распределение с математическими ожиданиями $\mu_1$ и $\mu_2$ и дисперсиями $\sigma_1^2$ и $\sigma_2^2$ соответственно, то $X_1+X_2$ также имеет нормальное распределение с математическим ожиданием $\mu_1+\mu_2$ и дисперсией $\sigma_1^2+\sigma_2^2$.

Моделирование нормальных случайных величин

Простейшие, но неточные методы моделирования основываются на центральной предельной теореме. Именно, если сложить много независимых одинаково распределённых величин с конечной дисперсией, то сумма будет распределена примерно нормально. Например, если сложить 12 независимых базовых случайных величин, получится грубое приближение стандартного нормального распределения. Тем не менее, с увеличением слагаемых распределение суммы стремится к нормальному.

Использование точных методов предпочтительно, поскольку у них практически нет недостатков. В частности, преобразование Бокса — Мюллера является точным, быстрым и простым для реализации методом генерации.

Центральная предельная теорема

Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:

• отклонение при стрельбе
• некоторые погрешности измерений (однако, многие погрешности приборов в технике имеют сильно не нормальные распределения)
• рост живых организмов

Такое широкое распространение закона связано с тем, что он является предельным законом, к которому приближаются многие другие (например, биномиальный).

Важно понимать, что использование гауссианы допустимо только при соблюдении следующих эмпирических условий: все факторы процесса известны (нет неизвестных или они несущественны), процесс немасштабируем (существуют верхние и нижние пределы), крайние события происходят не чаще, чем предсказывает правило 3-х сигм, и не имеют больших последствий. Таким образом, с помощью гауссианы некорректно моделировать социальные и экономические процессы. Однако хорошо поддаются моделированию большинство физических процессов.^[1]

Центральная предельная теорема показывает, что в случае, когда результат измерения (наблюдения) складывается под действием многих независимых причин, причем каждая из них вносит лишь малый вклад, а совокупный итог определяется аддитивно, то есть путём сложения, то распределение результата измерения (наблюдения) близко к нормальному.

См. также

• Аддитивный белый гауссовский шум
• Логнормальное распределение
• Центральная предельная теорема
• Двумерное нормальное распределение
• Многомерное нормальное распределение
• Статистический критерий

Ссылки

• Таблица значений функции стандартного нормального распределения

Примечания

1. ↑ Талеб Н. Н. Чёрный лебедь. Под знаком непредсказуемости. = The Black Swan: The Impact of the Highly Improbable. — КоЛибри, 2012. — 525 с. — ISBN 978-5-389-00573-0

	п·Вероятностные распределения
	Одномерные	Многомерные
Дискретные:	Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | дискретное равномерное	мультиномиальное
Абсолютно непрерывные:	Бета | Вейбулла | Гамма | гиперэкспоненциальное | Колмогорова | Коши | Лапласа | логнормальное | нормальное (Гаусса) | логистическое | Накагами |Парето | полукруговое | непрерывное равномерное | Райса | Рэлея | Стьюдента | Фишера | хи-квадрат | экспоненциальное | variance-gamma	многомерное нормальное | копула

Для улучшения этой статьи желательно?: Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное.