Распределение Стьюдента

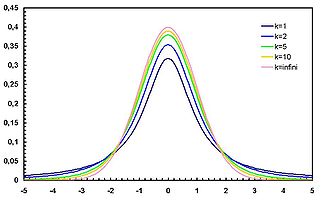
Распределение Стьюдента

Плотность вероятности
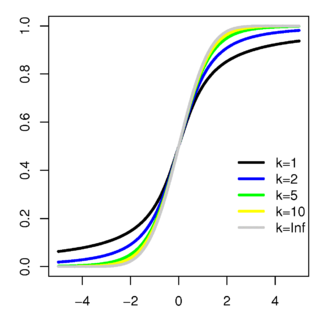
Функция распределения
Обозначение	{{{notation}}}
Параметры	$n > 0\!$ — число степеней свободы
Носитель	$x \in (-\infty; +\infty)\!$
Плотность вероятности	$\frac{\Gamma((n+1)/2)} {\sqrt{n\pi}\,\Gamma(n/2)\,(1+x^2/n)^{(n+1)/2}}\!$
Функция распределения	$\frac{1}{2} + \frac{x \Gamma \left( (n+1)/2 \right)}{\sqrt{\pi n}\,\Gamma (n/2)}$ $\frac{\,_2F_1 \left ( \frac{1}{2},(n+1)/2;\frac{3}{2};-\frac{x^2}{n} \right)} {\sqrt{\pi n}\,\Gamma (n/2)}$ где $\,_2F_1$ — гипергеометрическая функция
Математическое ожидание	$0\!$, если $n>1\!$
Медиана	$0\!$
Мода	$0\!$
Дисперсия	$\frac{n}{n-2}$, если $n>2\!$
Коэффициент асимметрии	$0\!$, если $n>3\!$
Коэффициент эксцесса	$\frac{6}{n-4}\!$, если $n>4\!$
Информационная энтропия	$\begin{matrix} \frac{n+1}{2}\left[ \psi(\frac{1+n}{2}) - \psi(\frac{n}{2}) \right] \\[0.5em] + \log{\left[\sqrt{n}B(\frac{n}{2},\frac{1}{2})\right]} \end{matrix}$ $\psi = \Gamma' / \Gamma$, $B$: бета-функция
Производящая функция моментов	не определена
Характеристическая функция

Распределе́ние Стью́дента в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений. Названо в честь Уильяма Сили Госсета, который первым опубликовал работы, посвящённые распределению, под псевдонимом «Стьюдент».

Определение

Пусть $Y_0,Y_1,\ldots, Y_n$ — независимые стандартные нормальные случайные величины, такие что $Y_i \sim \mathrm{N}(0,1),\; i=0,\ldots, n$. Тогда распределение случайной величины $t\!$, где

$t = \frac{Y_0}{\sqrt{\frac{1}{n}\sum\limits_{i=1}^n Y_i^2}},$

называется распределением Стьюдента с $n\!$ степенями свободы. Пишут $t \sim \mathrm{t}(n)\!$. Её распределение абсолютно непрерывно и имеет плотность

$f_t(y) = \frac{\Gamma\left(\frac{n+1}{2}\right)}{\sqrt{\pi n} \, \Gamma\left(\frac{n}{2}\right)}\, \left(1+\frac{y^2}{n}\right)^{-\frac{n+1}{2}}$,

где $\Gamma\!$ — гамма-функция Эйлера.

Свойства распределения Стьюдента

• Распределение Стьюдента симметрично. В частности если $t \sim \mathrm{t}(n)\!$, то $-t \sim \mathrm{t}(-n)\!$.

Моменты

Случайная величина $t \sim \mathrm{t}(n)\!$ имеет только моменты порядков $k < n\!$, причём

$\mathbb{E}\left[t^k\right] = 0$, если $k\!$ нечётно;

$\mathbb{E}\left[t^k\right] = \frac{\Gamma(\frac{k+1}{2})\Gamma(\frac{n-k}{2})n^{k/2}}{\sqrt{\pi}\Gamma(\frac{n}{2})}$, если $k\!$ чётно.

В частности,

$\mathbb{E}[t] = 0$,

$\mathrm{D}[t] = {n \over n - 2}$, если $n > 2\!$.

Моменты порядков $k \ge n$ не определены.

Связь с другими распределениями

• Распределение Коши является частным случаем распределения Стьюдента: $\mathrm{t}(1) \equiv \mathrm{C}(0,1)$.
• Распределение Стьюдента сходится к стандартному нормальному при $n \to \infty$. Пусть дана последовательность случайных величин $\{t_n\}_{n=1}^{\infty}$, где $t_n \sim \mathrm{t}(n),\; n \in \mathbb{N}$. Тогда: $t_n \to \mathrm{N}(0,1)$ по распределению при $n \to \infty$.
• Квадрат случайной величины, имеющей распределение Стьюдента, имеет распределение Фишера. Пусть $t \sim \mathrm{t}(n)$. Тогда: $t^2 \sim \mathrm{F}(1,n)$.

Применение распределения Стьюдента

Распределение Стьюдента используется в статистике для точечного оценивания, построения доверительных интервалов и тестирования гипотез, касающихся неизвестного среднего статистической выборки из нормального распределения. В частности, пусть $X_1,\ldots, X_n$ независимые случайные величины, такие что $X_i \sim \mathrm{N}(\mu, \sigma^2),\; i=1,\ldots, n$. Обозначим $\bar{X}$ выборочное среднее этой выборки, а $S^2$ её выборочную дисперсию. Тогда

$\frac{\bar{X} - \mu}{S / \sqrt{n}} \sim \mathrm{t}(n-1)$.

Процентили

Основная статья: Процентили распределения Стьюдента

Таблицы значений

Таблица значений функций распределения Стьюдента

	п·Вероятностные распределения
	Одномерные	Многомерные
Дискретные:	Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | дискретное равномерное	мультиномиальное
Абсолютно непрерывные:	Бета | Вейбулла | Гамма | гиперэкспоненциальное | Колмогорова | Коши | Лапласа | логнормальное | нормальное (Гаусса) | логистическое | Накагами |Парето | полукруговое | непрерывное равномерное | Райса | Рэлея | Стьюдента | Фишера | хи-квадрат | экспоненциальное | variance-gamma	многомерное нормальное | копула