Распределение хи-квадрат

Распределение $\chi^2$. Распределение Пирсона

Плотность вероятности
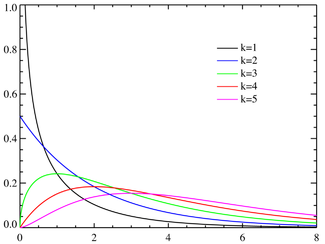
Функция распределения
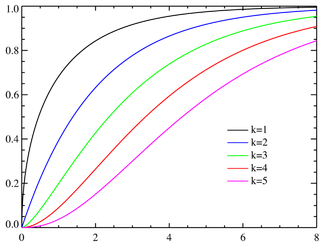
Обозначение	$\chi^2(k)\,$ или $\chi^2_k\,$
Параметры	$k > 0\,$ — число степеней свободы
Носитель	$x \in [0; +\infty)\,$
Плотность вероятности	$\frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}\,$
Функция распределения	$\frac{\gamma(k/2,x/2)}{\Gamma(k/2)}\,$
Математическое ожидание	$k\,$
Медиана	примерно $k-2/3\,$
Мода	$k-2\,$ если $n\geq 2\,$
Дисперсия	$2\,k\,$
Коэффициент асимметрии	$\sqrt{8/k}\,$
Коэффициент эксцесса	$12/k\,$
Информационная энтропия	$\frac{k}{2}\!+\!\ln\left[2\Gamma\left({k \over 2}\right)\right]\!+\!\left(1\!-\!\frac{k}{2}\right)\psi\left(\frac{k}{2}\right)$ $\!\psi(x) = \Gamma'(x) / \Gamma(x).$
Производящая функция моментов	$(1-2\,t)^{-k/2}$, если $2\,t<1\,$
Характеристическая функция	$(1-2\,i\,t)^{-k/2}\,$

Распределение $\chi^2$ (хи-квадрат) с $k$ степенями свободы — это распределение суммы квадратов $k$ независимых стандартных нормальных случайных величин.

Определение

Пусть $z_1, \ldots, z_k$ — совместно независимые стандартные нормальные случайные величины, то есть: $z_i \sim N(0,1)$. Тогда случайная величина

$x = z_1^2 + \cdots + z_k^2$

имеет распределение хи-квадрат с $k$ степенями свободы, то есть $x \sim f_{\chi^2(k)}(x)$.

Распределение хи-квадрат является частным случаем гамма-распределения, и имеет вид:

$f_{\chi^2(k)}(x) \equiv \Gamma\!\left({k \over 2}, {1 \over 2}\right) = \frac{(1/2)^{k \over 2}}{\Gamma\!\left({k \over 2}\right)}\, x^{{k \over 2} - 1}\, e^{-\frac{x}{2}}$,

где $\Gamma\!\left({k/2}, {1/2}\right)$ означает Гамма-распределение, а $\Gamma\!\left({k/2}\right)$ — Гамма-функцию.

Функция распределения имеет следующий вид:

$F_{\chi^2(k)}(x) = \frac{\gamma\left({k \over 2}, {x \over 2}\right)}{\Gamma\left({k \over 2}\right)}$,

где $\Gamma$ и $\gamma$ обозначают соответственно полную и неполную гамма-функции.

Свойства распределения хи-квадрат

• Распределение хи-квадрат устойчиво относительно суммирования. Если $\!Y_1, Y_2$ независимы, и $\!Y_1 \sim \chi^2(k_1)$, а $\!Y_2 \sim \chi^2(k_2)$, то

$\!Y_1 + Y_2 \sim \chi^2(k_1 + k_2)$.

• Из определения легко получить моменты распределения хи-квадрат. Если $Y \sim \chi^2(k)$, то

$\mathbb{E}[Y] = k$,

$\!\mathrm{D}[Y] = 2k$.

• В силу центральной предельной теоремы, при большом числе степеней свободы распределение случайной величины $Y \sim \chi^2(k)$ может быть приближено нормальным $Y \approx N( k, 2k )$. Более точно

$\frac{Y-k}{\sqrt{2k}} \to N(0,1)$ по распределению при $k \to \infty$.

Связь с другими распределениями

• Если $X_1 ,\ldots , X_k$ независимые нормальные случайные величины, то есть: $\,X_i \sim N(\mu,\sigma^2),\; i=1,\ldots, k;\; \mu$ известно, то случайная величина

$\,Y = \sum_{i=1}^k \left(\frac{X_i - \mu}{\sigma}\right)^2$

имеет распределение $\chi^2(k)$.

• Если $\!k=2$, то распределение хи-квадрат совпадает с экспоненциальным распределением:

$\chi^2(2) \equiv \mathrm{Exp}(1/2)$.

• Если $\,Y_1 \sim \chi^2(k_1)$ и $\,Y_2 \sim \chi^2(k_2)$, то случайная величина

$F = \frac{Y_1/k_1}{Y_2 / k_2}$

имеет распределение Фишера со степенями свободы $\!(k_1,k_2)$.

Процентили

Основная статья: Процентили распределения хи-квадрат

История

Критерий χ² был предложен Карлом Пирсоном (Pearson) в 1900 году.^[1] Его работа рассматривается как фундамент современной математической статистики. Предшественники Пирсона просто строили графики экспериментальных результатов и утверждали, что они правильны. В своей статье Пирсон привёл несколько интересных примеров злоупотреблений статистикой. Он также доказал, что некоторые результаты наблюдений за рулеткой (на которой он проводил эксперименты в течение двух недель в Монте-Карло в 1892 году) были так далеки от ожидаемых частот, что шансы получить их снова при предположении, что рулетка устроена добросовестно, равны одному из 10²⁹!

Общее обсуждение критерия χ² и обширную библиографию можно найти в обзорной работе Вильяма Дж. Кокрена.^[2]

См. также

• Критерий согласия Пирсона (критерий χ²)

Примечания

1. ↑ Karl Pearson. «On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling». Philosophical Magazine, Series 5 50 (302): 157-175. DOI:10.1080/14786440009463897.
2. ↑ William G. Cochran (1952). «The χ2 Test of Goodness of Fit». Annals Math. Stat. 23 (3): 315-345.

	п·Вероятностные распределения
	Одномерные	Многомерные
Дискретные:	Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | дискретное равномерное	мультиномиальное
Абсолютно непрерывные:	Бета | Вейбулла | Гамма | гиперэкспоненциальное | Колмогорова | Коши | Лапласа | логнормальное | нормальное (Гаусса) | логистическое | Накагами |Парето | полукруговое | непрерывное равномерное | Райса | Рэлея | Стьюдента | Фишера | хи-квадрат | экспоненциальное | variance-gamma	многомерное нормальное | копула