Гамма-распределение

Гамма-распределение

Плотность вероятности
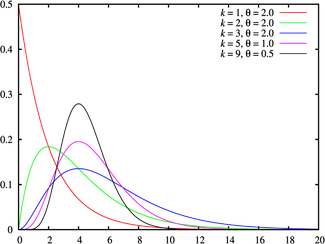
Функция распределения
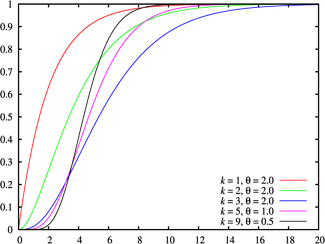
Обозначение	{{{notation}}}
Параметры	$k > 0,\,\theta > 0\,$ - коэффициент масштаба
Носитель	$x \in [0; \infty)\!$
Плотность вероятности	$x^{k-1} \frac{e^{-\frac{x}{\theta}}}{\Gamma(k)\theta^k}$
Функция распределения	$\frac{\gamma(k, x/\theta)}{\Gamma(k)}$
Математическое ожидание	$k \theta\,$
Медиана
Мода	$(k-1) \theta\,$, когда $k \geq 1\,$
Дисперсия	$k \theta^2\,$
Коэффициент асимметрии	$\frac{2}{\sqrt{k}}$
Коэффициент эксцесса	$\frac{6}{k}$
Информационная энтропия	$k\theta+(1-k)\ln(\theta)+\ln(\Gamma(k))\,$ $+(1-k)\psi(k)\,$
Производящая функция моментов	$(1 - \theta\,t)^{-k}$, когда $t < 1/\theta$
Характеристическая функция	$(1 - \theta\,i\,t)^{-k}$

Га́мма распределе́ние в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений. Если параметр $k$ принимает целое значение, то такое гамма-распределение также называется распределе́нием Эрла́нга.

Определение

Пусть распределение случайной величины $X$ задаётся плотностью вероятности, имеющей вид

$f_X(x) = \left\{ \begin{matrix} x^{k-1} \frac{e^{-x/\theta}}{\theta^k \, \Gamma(k)}, & x \ge 0 \\ 0, & x < 0 \end{matrix} \right.,$ где $\Gamma (k)$ - гамма-функция Эйлера.

Тогда говорят, что случайная величина $X$ имеет гамма-распределение с параметрами $k$ и $\theta$. Пишут $X \thicksim \Gamma(k,\theta)$.

Замечание. Иногда используют другую параметризацию семейства гамма-распределений. Или вводят третий параметр — сдвиг.

Моменты

Математическое ожидание и дисперсия случайной величины $X$, имеющей гамма-распределение, имеют вид

$\mathbb{E}[X] = k\theta$,

$\mathbb{D}[X] = k\theta^2$.

Свойства гамма-распределения

• Если $X_1,\ldots, X_n$ — независимые случайные величины, такие что $X_i \sim \Gamma(k_i, \theta),\; i = 1,\ldots, n$, то

$Y = \sum\limits_{i=1}^n X_i \sim \Gamma\left( \sum_{i=1}^n k_i, \theta \right)$.

• Если $X \thicksim \Gamma(k,\theta)$, и $a > 0$ — произвольная константа, то

$aX \thicksim \Gamma( k, a\theta)$.

• Гамма-распределение бесконечно делимо.

Связь с другими распределениями

• Экспоненциальное распределение является частным случаем гамма-распределения:

$\Gamma(1,1/\theta) \equiv \mathrm{Exp}(\theta)$.

• Если $X_1,\ldots,X_k$ — независимые экспоненциальные случайные величины, такие что $X_i \sim \mathrm{Exp}(\theta),\; i = 1,\ldots, k$, то

$Y = \sum\limits_{i=1}^k X_i \sim \Gamma(k,1/\theta )$.

• Распределение хи-квадрат является частным случаем гамма-распределения:

$\Gamma\left(\frac{n}{2},\frac{1}{2}\right) \equiv \chi^2(n)$.

• Согласно центральной предельной теореме, при больших $k$ гамма-распределение может быть приближено нормальным распределением:

$\Gamma(k, \theta) \approx \mathrm{N}(k\theta, k\theta^2)$ при $k \to \infty$.

• Если $X_1,X_2$ — независимые случайные величины, такие что $X_i \sim \Gamma(k_i,1),\; i=1,2$, то

$\frac{X_1}{X_1+X_2} \sim \mathrm{\Beta}(k_1,k_2)$.

Моделирование гамма-величин

Учитывая свойство масштабирования по параметру θ, указанное выше, достаточно смоделировать гамма-величину для θ = 1. Переход к другим значениям параметра осуществляется простым умножением.

Используя тот факт, что распределение $\Gamma (1, 1)$ совпадает с экспоненциальным распределением, получаем, что если U — случайная величина, равномерно распределённая на интервале (0, 1], то ${-\ln U} \sim \Gamma (1, 1)$.

Теперь, используя свойство k-суммирования, обобщим этот результат:

$\sum_{i=1}^n {-\ln U_i} \sim \Gamma (n, 1),$

где U_i — независимые случайные величины, равномерно распределённые на интервале (0, 1].

Осталось смоделировать гамма-величину для 0 < k < 1 и ещё раз применить свойство k-суммирования. Это является самой сложной частью.

Ниже приведён алгоритм без доказательства. Он является примером выборки с отклонением.

1. Положить m равным 1.
2. Сгенерировать $V_{2m - 1}$ и $V_{2m}$ — независимые случайные величины, равномерно распределённые на интервале (0, 1].
3. Если $V_{2m - 1} \le v_0$, где $v_0 = \frac e {e + \delta}$, перейти к шагу 4, иначе к шагу 5.
4. Положить $\xi_m = \left( \frac {V_{2m - 1}} {v_0} \right) ^{\frac 1 \delta}, \ \eta_m = V_{2m} \xi _m^ {\delta - 1}$. Перейти к шагу 6.
5. Положить $\xi_m = 1 - \ln {\frac {V_{2m - 1} - v_0} {1 - v_0}}, \ \eta_m = V_{2m} e^{-\xi_m}$.
6. Если $\eta_m > \xi_m^{\delta - 1} e^{-\xi_m}$, то увеличить m на единицу и вернуться к шагу 2.
7. Принять $\xi = \xi_m$ за реализацию $\Gamma (\delta, 1)$.

Подытожим:

$\theta \left( \xi - \sum _{i=1} ^{[k]} {\ln U_i} \right) \sim \Gamma (k, \theta),$

где [k] является целой частью k, а ξ сгенерирована по алгоритму, приведённому выше при δ = {k} (дробная часть k); U_i и V_l распределены как указано выше и попарно независимы.

	п·Вероятностные распределения
	Одномерные	Многомерные
Дискретные:	Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | дискретное равномерное	мультиномиальное
Абсолютно непрерывные:	Бета | Вейбулла | Гамма | гиперэкспоненциальное | Колмогорова | Коши | Лапласа | логнормальное | нормальное (Гаусса) | логистическое | Накагами |Парето | полукруговое | непрерывное равномерное | Райса | Рэлея | Стьюдента | Фишера | хи-квадрат | экспоненциальное | variance-gamma	многомерное нормальное | копула