Логистическое распределение

Логистическое распределение

Плотность вероятности
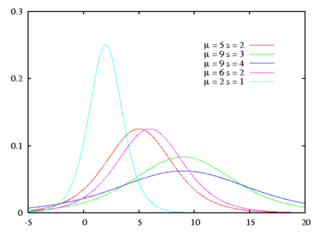
Функция распределения
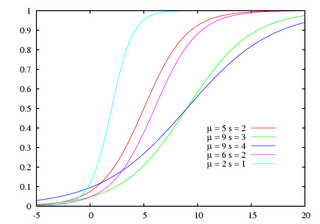
Обозначение	{{{notation}}}
Параметры	$\mu\,$ $s>0\,$
Носитель	$x \in (-\infty; +\infty)\!$
Плотность вероятности	$\frac{e^{-(x-\mu)/s}} {s\left(1+e^{-(x-\mu)/s}\right)^2}\!$
Функция распределения	$\frac{1}{1+e^{-(x-\mu)/s}}\!$
Математическое ожидание	$\mu\,$
Медиана	$\mu\,$
Мода	$\mu\,$
Дисперсия	$\frac{\pi^2}{3} s^2\!$
Коэффициент асимметрии	$0\,$
Коэффициент эксцесса	$6/5\,$
Информационная энтропия	$\ln(s)+2\,$
Производящая функция моментов	$e^{\mu\,t}\,\mathrm{B}(1-s\,t,\;1+s\,t)\!$ для $|s\,t|<1\!$, Бета-функция
Характеристическая функция	$e^{i \mu t}\,\mathrm{B}(1-ist,\;1+ist)\,$ для $|ist|<1\,$

Логисти́ческое распределе́ние в теории вероятностей и математической статистике — один из видов абсолютно непрерывных распределений. Формой напоминает нормальное распределение, но имеет более тяжелые концы и больший коэффициент эксцесса.

Определение

Функция плотности

Функция плотности вероятности логистического распределения задается формулой:

$f(x; \mu,s) = \frac{e^{-(x-\mu)/s}} {s\left(1+e^{-(x-\mu)/s}\right)^2} \!$

$=\frac{1}{4\,s} \;\operatorname{sech}^2\!\left(\frac{x-\mu}{2\,s}\right).$

Альтернативная параметризация задается подстановкой $\sigma^2 = \pi^2\,s^2/3$. Тогда функция плотности имеет вид:

$g(x;\mu,\sigma) = f(x;\mu,\sigma\sqrt{3}/\pi) = \frac{\pi}{\sigma\,4\sqrt{3}} \,\operatorname{sech}^2\!\left(\frac{\pi}{2 \sqrt{3}} \,\frac{x-\mu}{\sigma}\right).$

Функция распределения

Кумулятивной функцией распределения является логистическая функция:

$F(x; \mu,s) = \frac{1}{1+e^{-(x-\mu)/s}} \!$

$= \frac12 + \frac12 \;\operatorname{tanh}\!\left(\frac{x-\mu}{2\,s}\right).$

Квантили

Обратная функция к кумулятивной функции распределения ($F^{-1}$), обобщение logit функции:

$F^{-1}(p; \mu,s) = \mu + s\,\ln\left(\frac{p}{1-p}\right).$

Моменты распределения

Математическое ожидание

$E[X]=\int_{-\infty}^{\infty} {\frac{xe^{-(x-\mu)/s}} {s\left(1+e^{-(x-\mu)/s}\right)^2}} \! dx = \int_{-\infty}^{\infty} \frac{x}{4\,s} \;\operatorname{sech}^2\!\left(\frac{x-\mu}{2\,s}\right)dx$

Подставляем: $u=\frac{(x-\mu)}{2s}, du=\frac{1}{2s} dx$

$E[X]=\int_{-\infty}^{\infty} \frac{2\,s\,u+\mu}{2} \;\operatorname{sech}^2\!\left(u\right)du$

$E[X]=s\int_{-\infty}^{\infty} u \;\operatorname{sech}^2\!\left(u\right)du + \frac{\mu}{2} \int_{-\infty}^{\infty} \;\operatorname{sech}^2\!\left(u\right)du$

Справедливо равенство: $\int_{-\infty}^{\infty} u \;\operatorname{sech}^2\!\left(u\right)du = 0$

$E[X]=\frac{\mu}{2} \int_{-\infty}^{\infty} \;\operatorname{sech}^2\!\left(u\right)du = \frac{\mu}{2}\,2 = \mu$

Моменты высших порядков

Центральный момент n-го порядка может быть вычислен как:

$\begin{align} \operatorname{E}[(X-\mu)^n] &= \int_{-\infty}^\infty (x-\mu)^n dF(x) = \int_0^1 \big(F^{-1}(p)-\mu\big)^n dp \\ &= s^n \int_0^1 \Big[ \ln\!\Big(\frac{p}{1-p}\Big) \Big]^n \, dp. \end{align}$

Интеграл может быть выражен через числа Бернулли:

$\operatorname{E}[(X-\mu)^n] = s^n\pi^n(2^n-2)\cdot|B_n|.$

См. также

• Нормальное распределение

Литература

• N. Balakrishnan (1992). Handbook of the Logistic Distribution. Marcel Dekker, New York. ISBN 0-8247-8587-8.
• Johnson, N. L., Kotz, S., Balakrishnan N. (1995). Continuous Univariate Distributions. Vol. 2 (2nd Ed. ed.). ISBN 0-471-58494-0.

	п·Вероятностные распределения
	Одномерные	Многомерные
Дискретные:	Бернулли | биномиальное | геометрическое | гипергеометрическое | логарифмическое | отрицательное биномиальное | Пуассона | дискретное равномерное	мультиномиальное
Абсолютно непрерывные:	Бета | Вейбулла | Гамма | гиперэкспоненциальное | Колмогорова | Коши | Лапласа | логнормальное | нормальное (Гаусса) | логистическое | Накагами |Парето | полукруговое | непрерывное равномерное | Райса | Рэлея | Стьюдента | Фишера | хи-квадрат | экспоненциальное | variance-gamma	многомерное нормальное | копула

Для улучшения этой статьи желательно?: Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное.